Budowa grafów przyczynowo-skutkowych procesów z wykorzystaniem archiwalnych przebiegów sygnałów
Łukasz Tabor print
Metoda automatycznego tworzenia grafu przyczynowo-skutkowego procesu przemysłowego polega na wyszukiwaniu w całym zbiorze zmiennych procesowych takich sygnałów, które związane są pewnymi znanymi zależnościami, często występującymi w instalacjach przemysłowych (np. algorytm regulacji PID).
Następnie poszukiwane są pary sygnałów o wysokiej wartości współczynników korelacji liniowej Pearsona oraz monotonicznej Spearmana i Kendalla między zmiennymi. Dodatkowo analizowana jest sekwencja rozchodzenia się zaburzeń w instalacji. Na podstawie zdobytych informacji tworzony jest graf przyczynowo-skutkowy opisujący obiekt lub jego część. Przedstawiono efekt działania algorytmu dla dwóch obiektów. Pierwszy składa się z trzech zbiorników z cieczą z regulacją poziomu w jednym z nich. Drugim jest fragment sieci przesyłowej transportującej gaz ziemny na dużym obszarze.
O potrzebie budowy grafów przyczynowo-skutkowych
Grafy przyczynowo-skutkowe są graficzną reprezentacją zależności między wejściami (bodźcami) a odpowiadającymi im wyjściami (efektami). Informacje o występowaniu takich zależności mogą być przydatne w wielu zagadnieniach praktycznych. Na przykład, w procesie budowy modeli obiektów przemysłowych pierwszym etapem jest dobór odpowiedniej struktury, w szczególności wybranie spośród dostępnych sygnałów pomiarowych tych, które użyte zostaną jako wejścia powstającego modelu. Osoby zajmujące się takimi zagadnieniami często zmuszone są kierować się intuicją bądź sięgać po pomoc innych osób specjalizujących się w działaniu tej konkretnej instalacji, której model należy uzyskać.
Kolejnym przykładem zastosowania grafów jest analiza sekwencji występowania alarmów związanych z obiektami regulacji. Zazwyczaj jest tak, iż wejście instalacji w stan, który powoduje wystąpienie pewnego stanu alarmowego, powoduje także aktywowanie się innych alarmów w chwili bądź niedługo po wystąpieniu tego pierwszego. Dla operatora z kolei informacja o aktywnych kilkunastu lub kilkudziesięciu alarmach jest informacją mało przydatną. Do zadań projektantów systemów automatyki należy zatem odpowiednie filtrowanie takich sytuacji i wskazanie prawdziwego źródła wystąpienia sytuacji alarmowej [1].
Jeszcze inną dziedziną, w której omawiane grafy znajdują zastosowanie jest diagnostyka. Wiedząc o występowaniu zależności między sygnałami pomiarowymi oraz o miejscu ujawniania się wpływu uszkodzeń, można budować modele diagnostyczne [2, 3]. Informacja taka może być także przydatna w celu rekonfiguracji układu sterowania w przypadku wystąpienia awarii [4].
Procedura budowy grafu przyczynowo-skutkowego standardowymi metodami, w zależności od wielkości instalacji, może być bardzo trudna i niezwykle czasochłonna. W chwili obecnej proces ten opiera się na wykorzystaniu wiedzy eksperckiej. Specjalista w danej dziedzinie może opracować żądany graf wykorzystując swoją wiedzę oraz dokumentację techniczną obiektu. Pomimo tego w niektórych sytuacjach, ze względu na skomplikowanie zadania, może on nie być w stanie przewidzieć i określić wszystkich zależności. W każdym przypadku proces taki jest dość pracochłonny. Jednocześnie na współczesnych instalacjach przemysłowych działają systemy sterowania i wizualizacji procesów wykorzystujące bazy danych do przechowywania archiwalnych przebiegów sygnałów pomiarowych. Wiedza zawarta w takich bazach pozostaje na ogół niewykorzystana. Zawiera natomiast informacje o zależnościach potrzebnych w budowie grafu przyczynowo-skutkowego. Opisywana metoda ma za zadanie umożliwić automatyzację procesu tworzenia grafu za pomocą danych historycznych.
Algorytm budowy grafu
Proponowana metoda składa się z trzech etapów: wyszukiwanie zależności o znanym charakterze (często występujących w obiektach przemysłowych), wyszukiwanie sygnałów zależnych oraz obserwacja propagacji zakłóceń w instalacji.
Zależności o znanym charakterze
Każda instalacja przemysłowa składa się z bardzo dużej liczby elementów. Wiele z nich to standardowe urządzenia, których zasada działania jest powszechnie znana. Dostępne są również równania opisujące powiązania sygnałów wejściowych i wyjściowych takich urządzeń. Skoro znamy charakter tych zależności, to można przeszukać posiadaną bazę danych i w przypadku znalezienia sygnałów spełniających daną równość sądzić, że sygnały te opisują takie urządzenie. Przykładem dobrze znanego i powszechnie występującego związku jest powiązanie strumienia cieczy przepływającego przez zawór oraz różnicy ciśnień na jego końcach i stopnia otwarcia. Innym przykładem wyjaśniającym algorytm postępowania na tym etapie budowy grafu jest regulator typu PID. Sygnał wyjściowy (CV) idealnego regulatora w chwili t jest związany, zgodnie z zależnością (1), z różnicą między wartością zadaną (SP) i wielkością regulowaną (PV).
| (1) |
| (2) |
Algorytm w tym przypadku losuje z dostępnego zbioru trzy sygnały. Następnie odejmuje od siebie dwa z nich, tworząc zmienną e. Kolejnym krokiem jest wyznaczenie pomocniczych sygnałów ei oraz ed, z których pierwszy jest całką, a drugi pochodną po czasie z e (de/dt). Algorytm przeprowadza test regresji wielowymiarowej [6], gdzie zmienną objaśnianą jest nieużyty do tej pory sygnał z wybranej pierwotnie trójki, a zmiennymi objaśniającymi e, ei, ed. W przypadku występowania zależności liniowej przyjmuje się, że w danym miejscu instalacji umieszczony jest regulator PID. W przeciwnym - powtarza się algorytm od momentu obliczenia odchyłki e, wybierając inną kombinacje sygnałów z wybranej trójki lub nową trójkę, aż do przeszukania całej przestrzeni dostępnych zmiennych.
Wyszukiwanie sygnałów zależnych probabilistycznie
Po odnalezieniu zależności o znanym charakterze następuje poszukiwanie par zmiennych o wysokich współczynnikach zależności probabilistycznych. Podejście to wynika z faktu, że prawdopodobieństwo istnienia współzależności między sygnałami pochodzącymi z „bliskich” sobie części instalacji jest większe niż dla odległych od siebie części procesu. Jako miarę podobieństwa sygnałów wykorzystano trzy miary zależności probabilistycznej.
1. Współczynnik korelacji Pearsona [5, 6, 7]:
| (3) |
gdzie: x, y – badane sygnały, n – długość wektorów x, y.
Miara ta jest wrażliwa na występowanie sygnałów liniowo zależnych. W związku z tym, iż w rzeczywistych obiektach zazwyczaj mamy do czynienia z zależnościami nieliniowymi, skorzystano z podanego niżej współczynnika.
2. Współczynnik korelacji rang Spearmana [5, 6, 7]:
S – liczony wg wzoru (3) z tą różnicą, że zamiast wartości sygnałów xi, yi wstawia się rangi będące indeksem danej obserwacji po uszeregowaniu konkretnego sygnału od wartości najmniejszych do największych. Miara taka jest bardziej odporna od poprzedniego współczynnika na nieliniowości, a także łatwiej radzi sobie z obserwacjami odstającymi. Mimo to wykorzystano jeszcze trzecią miarę.
3. Współczynnik K Kendalla [5, 6, 7]:
| (4) |
gdzie: P – liczba par zgodnych (oba sygnały maleją lub oba rosną), Q – liczba par niezgodnych (jeden sygnał maleje, drugi rośnie), T – pary wiązane (pozostałe przypadki). Miara ta jest wrażliwa na każdą zależność, która jest monotoniczna. Założenie takie jest spełnione w większości zależności występujących dla obiektów przemysłowych.
Dla każdej miary ustalana jest progowa jej wartość, powyżej której algorytm stwierdza występowanie zależności.
Obserwacja propagacji zakłóceń
Ten etap w dużej mierze związany jest z poprzednim, gdyż wykorzystuje te same miary. Jednak tym razem wyznaczane jest przesunięcie jednego sygnału względem drugiego, dla którego wymienione współczynniki osiągają maksimum. Otrzymane wartości przesunięć mówią o opóźnieniach transportowych między sygnałami. Sposób, w jaki wyznaczone opóźnienia wykorzystywane są w budowie grafu, omówiony zostanie na przykładzie.
Przykład 1 – układ trzech zbiorników
Działanie algorytmu zostanie pokazane na przykładzie prostego obiektu, jakim jest układ trzech zbiorników z cieczą (rys. 1). Zbiorniki połączone są kanałami umożliwiającymi przepływ cieczy między nimi. Trzeci zbiornik ma kanał odprowadzający. Do pierwszego zbiornika dostarczana jest ciecz za pomocą pompy i zaworu regulacyjnego. Układ ma za zadanie regulować poziom w trzecim zbiorniku. Do tego celu wykorzystano regulator PID. Na stanowisku są dostępne oraz archiwizowane pomiary poziomu cieczy w zbiornikach L1, L2, L3, wyjście z regulatora CV oraz wartość zadana poziomu SP.
Dla zaprezentowania działania algorytmu przeprowadzono symulację normalnej pracy instalacji zmieniając wartość zadaną. Zarchiwizowane przebiegi pięciu wspomnianych sygnałów poddano działaniu algorytmu w celu uzyskania grafu. Pierwszy etap algorytmu wykrył istnienie zależności charakterystycznej dla regulatora PID miedzy sygnałami L3, SP oraz CV. Na tej podstawie powstał zalążek grafu widoczny na rys. 2.
W kolejnym kroku zbadano wartości miar zależności probabilistycznych wymienionych w poprzednim rozdziale. Wykryto, że pary (L1, L3), (L2, L3) charakteryzują się dużą wartością wszystkich współczynników. Rozbudowano zatem graf do postaci z rys. 3. Jednocześnie wykryto zależność w parze (L1, L2). Zbadano możliwe opóźnienia między wspomnianymi parami sygnałów. Zachowanie się współczynników korelacji w funkcji przesunięcia sygnałów przedstawia rys. 4.
Odczytano przesunięcia, dla których występowało maksimum miar zależności. Okazało się, iż opóźnienie między sygnałami L1 i L3 jest sumą opóźnień między L1 a L2 i L2 a L3. Z tego powodu zmodyfikowano poprzedni graf do postaci z rys. 5.
Do zakończenia procesu tworzenia grafu pozostało jeszcze określenie, na który sygnał oddziałuje w pierwszej kolejności sygnał CV. Do tej pory stwierdzono jedynie, iż musi być to któryś z sygnałów mających wpływ na L3 bądź bezpośrednio L3. W tym celu wyznaczono opóźnienia między sygnałem CV a L1, L2, L3. Efekt przedstawia rys. 6. Odczytano, iż w pierwszej kolejności na zmianę sygnału CV reaguje L1. Graf musi mieć zatem postać z rys. 7.
Przykład 2 – sieć gazowa
Przykładem obiektu przemysłowego, na którym testowano działanie algorytmu jest fragment sieci przesyłającej gaz na dużym obszarze Polski. Fragment ten obejmuje rurociąg główny wraz z odnogami, które zakończone są osiemnastoma stacjami poboru gazu. W większości z takich stacji dokonywane są pomiary takich parametrów gazu, jak przepływ, ciśnienie oraz temperatura. Niestety w niektórych stacjach nie wszystkie pomiary są realizowane. Do budowy grafu postanowiono wykorzystać pomiary ciśnień. Schemat sieci z zaznaczonymi na czerwono stacjami, w których pomiar ciśnienia nie był rejestrowany przedstawiono na rys. 8.
Po uwzględnieniu braków sygnałowych w wyniku działania algorytmu należałoby się spodziewać otrzymania grafu przedstawionego na rys. 9.
W trakcie realizacji algorytmu dla tego przykładu okazało się, jak newralgicznym punktem metody może być dobór właściwych progów miar probabilistycznych w etapie drugim. Uzyskane grafy dla różnych wartości tych współczynników przedstawiono na rys. 10 i 11.
Podsumowanie
Grafy przyczynowo-skutkowe obiektów przemysłowych mogą stanowić istotne udogodnienie w pracy specjalistom w wielu dziedzinach. Obecnie proces tworzenia grafu jest żmudny i kosztowny. Istnieje natomiast możliwość wydobycia informacji o zachodzeniu zależności między zmiennymi z historycznych przebiegów sygnałów pomiarowych. Metoda, jak pokazały przykłady, może prowadzić do obiecujących wyników, jednak wymaga dalszych prac. Kwestią priorytetową jest opracowanie inteligentnego procesu doboru krytycznych wartości miar zależności dla każdego węzła. Innym problemem do pokonania jest możliwość występowania w obiekcie sygnałów dyskretnych.
Zaprezentowane w artykule podejście można rozwinąć wykorzystując wiedzę zawartą w dokumentacji technicznej bądź oznaczeniach zmiennych procesowych. Rozważać można niekiedy wykorzystanie eksperymentów czynnych do obserwacji rozchodzenia się zaburzeń w obiekcie.
Bibliografia
- Gandhi O.P., Agrawal, V.P.: Failure cause analysis – a structural approach, Journal of Pressure Vessel Technology, Transactions of the ASME, 4/1996, 434–439.
- Ostasz A.: Graf przyczynowo-skutkowy procesu i jego zastosowanie do projektowania zbioru residuów oraz relacji diagnostycznej. Politechnika Warszawska, 2007.
- Ostasz A., Kościelny J.M.: Zastosowanie grafu procesu GP w diagnostyce procesów przemysłowych. Pomiary Automatyka Kontrola nr 9bis/2005, 51–53.
- Garcia-Beltran C., Gentil S.: Casual reasoning for human supervised process reconfiguration. IEEE International Symposium on Intelligent Control – Proceedings, 2001, 91-96.
- Koronacki J., Mielniczuk J.: Statystyka dla studentów kierunków technicznych i przyrodniczych. WNT, Warszawa 2007.
- Larose D. T. Metody i modele eksploracji danych. PWN, Warszawa 2008.
- Krzyśko M.: Systemy uczące się: rozpoznawanie wzorców, analiza skupień i redukcja wymiarowości. WNT, Warszawa 2008.
mgr inż. Łukasz Tabor
Jest doktorantem w Instytucie Automatyki i Robotyki na Wydziale Mechatroniki Politechniki Warszawskiej. Ukończył studia na kierunku Automatyka i Robotyka. W ramach prac naukowo-badawczych zajmuje się modelowaniem i diagnostyką procesów przemysłowych.
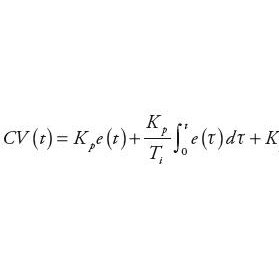
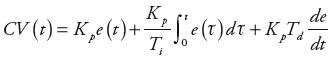
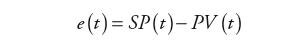
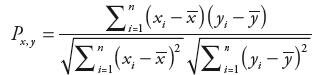
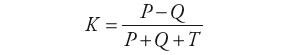
![Rys. 1. Układ trzech zbiorników [The three tank system] Rys. 1. Układ trzech zbiorników [The three tank system]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r1.jpg/76999-1-pol-PL/r1.jpg_large.jpg)
![Rys. 2. Graf po etapie 1 [The graph after stage 1] Rys. 2. Graf po etapie 1 [The graph after stage 1]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r2.jpg/77002-1-pol-PL/r2.jpg_medium.jpg)
![Rys. 3. Kolejny etap powstawania grafu [The next stage of graph formation] Rys. 3. Kolejny etap powstawania grafu [The next stage of graph formation]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/3_300.jpg/77005-1-pol-PL/3_300.jpg_large.jpg)



![Rys. 5. Graf po etapie 3 [The graph after stage 3] Rys. 5. Graf po etapie 3 [The graph after stage 3]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/5_300.jpg/77017-1-pol-PL/5_300.jpg_medium.jpg)
![Rys. 6. Wyznaczenie opóźnień względem CV [Determination of the delays time with respect to CV] Rys. 6. Wyznaczenie opóźnień względem CV [Determination of the delays time with respect to CV]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r6.jpg/77020-1-pol-PL/r6.jpg_medium.jpg)
![Rys. 7. Ostateczna postać grafu przyczynowo-skutkowego dla układu trzech zbiorników [The final form of the causal graph for the three tank system] Rys. 7. Ostateczna postać grafu przyczynowo-skutkowego dla układu trzech zbiorników [The final form of the causal graph for the three tank system]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r7.jpg/77023-1-pol-PL/r7.jpg_medium.jpg)
![Rys. 8. Schemat sieci gazowej - na czerwono zaznaczono stacje, w których brakuje pomiaru ciśnienia [The schematic diagram of gas network - stations without pressure measurement are marked with red color] Rys. 8. Schemat sieci gazowej - na czerwono zaznaczono stacje, w których brakuje pomiaru ciśnienia [The schematic diagram of gas network - stations without pressure measurement are marked with red color]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r8.jpg/77026-1-pol-PL/r8.jpg_medium.jpg)
![Rys. 9. Graf sieci sporządzony z wykorzystaniem wiedzy eksperckiej [The network graph designed by using the experts knowledge] Rys. 9. Graf sieci sporządzony z wykorzystaniem wiedzy eksperckiej [The network graph designed by using the experts knowledge]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r9.jpg/77029-1-pol-PL/r9.jpg_medium.jpg)
![Rys. 10. Wynik działania algorytmu dla współczynnika odcięcia 0,95 [The result of the algorithm for 0,95 cutoff value] Rys. 10. Wynik działania algorytmu dla współczynnika odcięcia 0,95 [The result of the algorithm for 0,95 cutoff value]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r10.jpg/77032-1-pol-PL/r10.jpg_large.jpg)
![Rys. 11. Wynik działania algorytmu dla współczynnika odcięcia 0,97. Na czarno zaznaczono zależności prawidłowo wykryte, na czerwono nieprawidłowo sklasyfikowane, linią kropkowaną relacje bliskie prawdzie [The result of the algorithm for 0,97 cutoff value. The dependence correctly detected are marked with black color, incorrectly classified by red color and closely match to the true relationship by dotted line] Rys. 11. Wynik działania algorytmu dla współczynnika odcięcia 0,97. Na czarno zaznaczono zależności prawidłowo wykryte, na czerwono nieprawidłowo sklasyfikowane, linią kropkowaną relacje bliskie prawdzie [The result of the algorithm for 0,97 cutoff value. The dependence correctly detected are marked with black color, incorrectly classified by red color and closely match to the true relationship by dotted line]](https://automatykaonline.pl/var/aol/storage/images/media/par/11_10/tabor/r11.jpg/77035-1-pol-PL/r11.jpg_large.jpg)