Obliczanie niepewności pomiaru zgodne z definicją przedziału rozszerzenia na przykładzie opracowania wyniku wzorcowania mikrometru
Paweł Fotowicz print
W artykule przedstawiono obliczenia niepewności rozszerzonej metodą numeryczną i analityczną. Obie metody umożliwiają wyznaczanie niepewności zgodnie z przyjętą definicją przedziału rozszerzenia zawartą w najnowszym dokumencie normatywnym.
Metoda numeryczna polega na symulacji Monte Carlo, a metoda analityczna bazuje na przybliżeniu operacji splotu rozkładów wielkości wejściowych, poprzez model matematyczny dla wielkości wyjściowej. Obie metody prowadzą do tego samego rezultatu obliczeniowego i można je realizować przy użyciu arkusza kalkulacyjnego. Metody zilustrowano przykładem opracowania wyniku pomiaru przy wzorcowaniu przyrządu pomiarowego − mikrometru.
We współczesnej metrologii następują istotne zmiany w podejściu do opracowywania wyniku pomiaru [1]. Klasyczne prawo propagacji niepewności zastępowane jest zasadą propagacji rozkładów, realizowaną przez model matematyczny wielkości mierzonej, a miarą niepewności jest przedział rozszerzenia. W tradycyjnym podejściu miarą niepewności jest niepewność rozszerzona obliczana jako iloczyn współczynnika rozszerzenia i złożonej niepewności standardowej [2]. Nowe rozwiązania opierają się na definicji przedziału rozszerzenia, którego granice wyznaczają kwantyle rozkładu prawdopodobieństwa związanego z wielkością mierzoną [3]. Parametry tego rozkładu są wyznaczane na ogół metodą numeryczną przy użyciu symulacji Monte Carlo. Postępowanie polega na zastosowaniu procedury z użyciem generatora liczb losowych.
Obliczenia metodą numeryczną
Procedurę obliczeniową można wykonać przy użyciu arkusza kalkulacyjnego Excel, wyposażonego we wbudowaną funkcję o nazwie „los”. Funkcja ta oddaje zbiór wartości losowych z zakresu od 0 do 1 o rozkładzie równomiernym. Należy tę funkcję przekształcić do postaci umożliwiającej generowanie zbiorów o typowych rozkładach prawdopodobieństwa, takich jak rozkład prostokątny, trójkątny, normalny czy Studenta, które stosuje się do opisu wielkości wejściowych.
| (1) | |
| (2) | |
| (3) |
Uzyskanie rozkładu Studenta wymaga zastosowania dwóch kroków postępowania. W pierwszym generujemy zbiór wartości o rozkładzie normalnym standaryzowanym N(0, 1), a w drugim − zbiór wartości zmiennej losowej t o rozkładzie Studenta
| (4) |
gdzie n jest liczbą obserwacji,
średnią zbioru obserwacji, a s(x) odchyleniem standardowym eksperymentalnym tego zbioru.
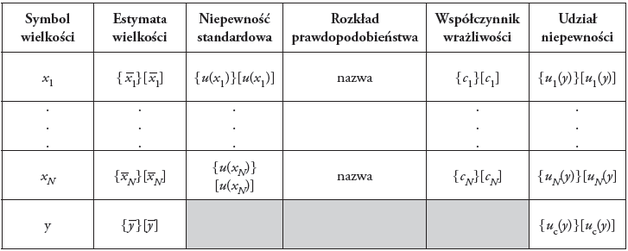
W przypadku pomiarów wzorcujących mamy do czynienia z liniowym lub linearyzowanym równaniem pomiaru, które w ogólnej postaci przyjmuje formę
| (5) |
gdzie y to wielkość wyjściowa będąca wielkością wzorcowaną lub błędem wskazania przyrządu pomiarowego,
jej estymata, δxi wielkości wpływające, a ci współczynniki wrażliwości. Wielkości te są powiązane z odpowiednimi wielkościami budżetu niepewności (tab. 1).
Każdą z wielkości wejściowych xi można przedstawić w postaci sumy jej estymaty
jako wartości stałej oraz części zmiennej δxi
| (6) |
W praktyce większość wielkości wejściowych charakteryzuje się zerową wartością estymaty, pełniąc rolę wielkości wpływających.
Zbiory wartości części zmiennych δxi wielkości wejściowych można wyznaczyć przy użyciu funkcji:
δxi = P(0, u) dla wielkości o rozkładzie prostokątnym
δxi = T(0, u) dla wielkości o rozkładzie trójkątnym
δxi = N(0, u) dla wielkości o rozkładzie normalnym
δxi = S(0, u) dla wielkości o rozkładzie Studenta.
W praktyce obliczeniowej jako u najlepiej przyjąć udział niepewności ui(y). Wówczas zmienne δxi zawierają również współczynnik wrażliwości ci, a równanie pomiaru sprowadza się do postaci addytywnej
| (7) |
Estymatę wielkości wyjściowej można wyznaczyć jako funkcję estymat wielkości wejściowych, na podstawie równania pomiaru
| (8) |
Mając wyznaczone wszystkie wielkości zapisane w tabeli budżetu niepewności, możemy przystąpić do obliczeń wielkości wyjściowej metodą propagacji rozkładów przy użyciu symulacji Monte Carlo. W kolejnych kolumnach arkusza wpisujemy odpowiednie formuły obliczające wartości zgodne z odpowiednimi rozkładami dla wielkości wejściowych: prostokątnym, trójkątnym, normalnym lub Studenta. W oddzielnej kolumnie wykonujemy obliczenia równania pomiaru, wprowadzając do każdej komórki tej kolumny sumę estymaty wielkości wyjściowej
i możliwych wartości dla wszystkich wielkości wejściowych δxi zgodnie z przyjętymi rozkładami prawdopodobieństwa. Ponieważ w kolumnie tej zapisane są formuły realizujące równanie pomiaru, należy ją przekopiować do innej kolumny w postaci samych wartości liczbowych (operacja: wklej specjalnie – wartości). Następnie sortujemy zbiór tych wartości od najmniejszej do największej (operacja: sortuj rosnąco). W kolumnie obok możemy również wpisać kolejne prawdopodobieństwa, zaczynając od wartości p=0,0001, a kończąc na wartości p=1 z krokiem 0,0001. W ten sposób możemy zobrazować, przy użyciu operacji: wstaw wykres (punktowy), dystrybuantę numeryczną rozkładu prawdopodobieństwa związanego z wielkością wyjściową.
Z posortowanego zbioru wartości dla wielkości wyjściowej odczytujemy zawartość komórek 250 i 9750. Komórki te przedstawiają wartości dolnej i górnej granicy przedziału rozszerzenia dla prawdopodobieństwa 95 %. Odejmując od wartości górnej granicy jej wartość dolną i dzieląc wynik przez dwa otrzymujemy niepewność rozszerzoną dla prawdopodobieństwa 95 %.
Wykonując obliczenia w arkuszu można również skorzystać z narzędzi analizy danych zawartych w dodatku Analysis ToolPak w postaci generatorów liczb pseudolosowych o różnych rozkładach. Szczególnie przydatny może być generator o rozkładzie jednostajnym i normalnym, co można wykorzystać przy realizacji obliczeń metodą Monte Carlo.
Przykład obliczeniowy
Jako przykład obliczeniowy można przedstawić opracowanie wyniku wzorcowania mikrometru przy użyciu płytki wzorcowej. Równanie pomiaru, w postaci błędu wskazania mikrometru, ma postać
| (9) |
gdzie: l – długość płytki zmierzona mikrometrem, δl – rozdzielczość pomiaru mikrometrem, lw– długość płytki wzorcowej, δlt – poprawka temperaturowa.
W równaniu występują cztery wielkości wejściowe:
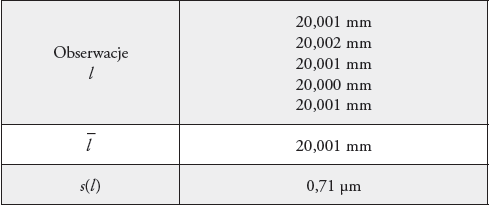
1) Długość płytki zmierzona mikrometrem – l
Wykonano pięć pomiarów różnicowych długości płytki wzorcowej, za każdym razem zerując wskazanie mikrometru, których wyniki zestawiono w tab. 2.
Estymatą wielkości jest średnia serii n=5 obserwacji, a miarą niepewności standardowej jest odchylenie standardowe eksperymentalne tej średniej
| (10) |
Z wielkością tą związany jest rozkład Studenta o liczbie stopni swobody v = n – 1 = 4.
2) Rozdzielczość pomiaru mikrometrem – δl
Należy uwzględnić jednocześnie rozdzielczość ustawienia zera mikrometru i odczytu na płytce wzorcowej, która wynosi 1 µm. W przypadku pomiaru różnicowego sumaryczna rozdzielczość opisana jest rozkładem trójkątnym powstającym ze złożenia dwóch rozkładów prostokątnych, w punkcie zerowania i na wzorcu. Niepewność standardowa wynosi
| (11) |
3) Długość płytki wzorcowej – lw
W świadectwie wzorcowania płytki wzorcowej podano, że długość jej wynosi: lw=20,0002 mm i została wyznaczona z niepewnością rozszerzoną U=0,1 µm przy współczynniku rozszerzenia k=2 dla poziomu ufności 95 %. Niepewność standardowa wynosi
| (12) |
4) Poprawka temperaturowa – δlt
W trakcie pomiaru temperatura mogła zmienić się w granicach: ±1 °C, a współczynnik rozszerzalności cieplnej materiału płytki wzorcowej wynosi: 12·10-6 °C-1. Niepewność standardowa t
| (13) |
Wszystkie wielkości zestawiono w tabeli budżetu niepewności (tab. 3).
| Symbol wielkości | Estymata wielkości | Niepewność standardowa | Rozkład prawdopodobieństwa | Współczynnik wrażliwości | Udział niepewności |
| l | 20,001 mm | 0,32 µm | Studenta (v = 4) | 1 | 0,32 µm |
| δl | 0 mm | 0,41 µm | trójkątny | 1 | 0,41 µm |
| lw | 20,0002 mm | 0,05 µm | normalny | -1 | -0,05 µm |
| δlt | 0 mm | 0,14 µm | prostokątny | -1 | -0,14 µm |
| e | 0,0008 mm | 0,54 µm |
Wszystkie obliczenia wykonywane są w arkuszu kalkulacyjnym. Widok strony obliczeniowej przedstawiono na rys. 1. Dane wejściowe wprowadzane są do tabeli budżetu. Arkusz oblicza niepewności standardowe, udziały niepewności i złożoną niepewność standardową. W kolumnach od M do P obliczane są zbiory wartości wielkości wejściowych o przyjętych rozkładach prawdopodobieństwa. W kolumnie L generowany jest zbiór wartości o rozkładzie normalnym standaryzowanym, aby na jego podstawie w kolumnie M wyznaczyć zbiór zmiennej t o rozkładzie Studenta z liczbą stopni swobody v=4 i odpowiednim udziale niepewności charakterystycznym dla pierwszej wielkości wejściowej. W kolumnie N wyznaczany jest zbiór wartości o rozkładzie trójkątnym z udziałem niepewności charakterystycznym dla drugiej wielkości wejściowej, podobnie w kolejnych kolumnach O i P zbiory wartości o rozkładzie normalnym i prostokątnym oraz odpowiednich udziałach niepewności charakterystycznych dla trzeciej i czwartej wielkości wejściowej. W kolumnie Q realizowane jest równanie pomiaru. Zawartość tej kolumny w postaci wartości liczbowych kopiowana jest do kolumny S, a jej zawartość sortowana jest rosnąco. W kolumnie T posortowanym wartościom wielkości wyjściowej przypisywane są kolejne prawdopodobieństwa, zaczynając od 0,0001. Na podstawie zbiorów wartości zawartych w sąsiednich kolumnach S i T możemy wykreślić przebieg dystrybuanty numerycznej zbioru możliwych wartości błędu wskazania mikrometru (rys. 2). Dodatkowo można również wyznaczyć histogram powyższego zbioru (rys. 3) poprzez opcję Histogram (dodatek Analysis ToolPak) lub przy użyciu funkcji arkusza o nazwie częstość.
Na podstawie zbioru danych wyjściowych (kolumna S) obliczana jest wartość średnia jako miara błędu pomiaru e oraz granice przedziału rozszerzenia tego błędu: dolna elow i górna ehigh. Wartość dolnej granicy błędu zawarta jest w komórce o adresie S250, a wartość górnej granicy w komórce o adresie S9750. Na tej podstawie można wyznaczyć długość przedziału rozszerzenia
| (14) |
Niepewność rozszerzona jest połową przedziału rozszerzenia
| (15) |
Wynik wzorcowania można zapisać w postaci błędu wskazania mikrometru dla płytki wzorcowej o długości 20 mm, który wynosi (0,8 ±1,2) µm.
Porównanie wyniku z obliczeniami metodą analityczną
Do wyznaczania niepewności rozszerzonej zgodnie z przyjętymi definicjami przedziału rozszerzenia opracowano metodę analityczną opartą na splocie rozkładów wielkości wejściowych [4]. Jej aplikację przedstawiono w artykule [5]. Metodę łatwo implementuje się do arkusza kalkulacyjnego. Metoda polega na zastosowaniu przybliżonego wzoru na niepewność rozszerzoną postaci
| (16) |
gdzie kPN to kwantyl rozkładu typu P*N [5], t(v) to kwantyl rozkładu Studenta z liczbą stopni swobody v, kN to kwantyl rozkładu normalnego (kN=1,96 dla prawdopodobieństwa 95 %). Wartości współczynnika kPN dla prawdopodobieństwa 95 % zostały przedstawione w publikacjach [4, 5] w funkcji ilorazu udziału niepewności
| (17) |
gdzie ui(y)max to największy udział niepewności wielkości wejściowej o rozkładzie prostokątnym.
Widok strony obliczeniowej pokazano na rys. 4. Tabela budżetu zawiera dodatkową kolumnę z liczbą stopni swobody. W kolumnie M wyznaczany jest największy udział o rozkładzie prostokątnym (w przykładzie obliczeniowym wnosi go składowa prostokątna rozkładu trójkątnego). W kolumnie N wyznaczany jest pierwiastek z sumy kwadratów udziałów, odpowiednio zgodnie z wzorem (16), powiększony o iloraz kwantyla rozkładu Studenta do kwantyla rozkładu normalnego. W kolumnie O zapisano wartości współczynników kPN, a w kolumnie P wartości graniczne dla ilorazu niepewności [4]. Kolumna Q zawiera wartości obliczonego ilorazu niepewności ru. W kolumnie R przy użyciu funkcji logicznych przepisywana jest wartość kPN, gdy rujest mniejsze od wartości granicznej lub zero, gdy ru jest większe od tej wartości. Za pomocą funkcji max wybierana jest największa wartość współczynnika kPN, która pozwala na obliczenie niepewności rozszerzonej U (w komórce o adresie I13). Dodatkowo wyznaczana jest wartość współczynnika rozszerzenia k dla wielkości wyjściowej (w komórce o adresie D13).
Wynik pomiaru otrzymany metodą analityczną, w postaci błędu wskazania mikrometru dla płytki wzorcowej o długości 20 mm, wynosi (0,8 ±1,2) µm i liczbowo nie różni się od wyniku otrzymanego metodą numeryczną. Nie oznacza to jednak, iż niepewności rozszerzone w obu przypadkach obliczeń są takie same. Niepewność rozszerzona przedstawiona z czterema miejscami znaczącymi przyjmuje wartość U=1,187 µm (komórka I15, rys. 1), przy obliczeniach metodą numeryczną i wartość U=1,216 µm (komórka I13, rys. 4), przy obliczeniach metodą analityczną. Względna różnica pomiędzy tymi wartościami wynosi 2,5 %, co nie ma wpływu na wartość niepewności rozszerzonej, gdy wyrażamy ją z dwoma cyframi znaczącymi, w postaci U=1,2 µm.
Podsumowanie
Przedstawiona metoda obliczeniowa niepewności pomiaru ma na celu wyznaczanie jej zgodnie z przyjętymi międzynarodowymi definicjami przedziału rozszerzenia stosowanymi we współczesnej metrologii. Metoda ta jest oparta na symulacji Monte Carlo, którą można realizować przy użyciu generatora liczb losowych dostępnego w arkuszu kalkulacyjnym. Nie wymaga przy tym stosowania specjalistycznego oprogramowania i przez to dostępna jest dla każdego użytkownika komputera osobistego. Może być stosowana w każdym laboratorium pomiarowym, nie tylko zajmującym się wzorcowaniem przyrządów pomiarowych. Równolegle z algorytmem numerycznym można stosować metodę analityczną dającą ten sam wynik obliczeniowy, gdy niepewność rozszerzoną wyrażamy z zalecanymi dwoma cyframi znaczącymi.
Opisane postępowanie może mieć również dodatkowy aspekt. Zalecenia dokumentu [3] mówią o konieczności wykonywania obliczeń niepewności rozszerzonej taką metodą, której wynik obliczeniowy da się zwalidować metodą Monte Carlo, jako metodą odniesienia. Można zatem obie techniki stosować przy obliczeniach równolegle, a wynik obliczeń metodą numeryczną traktować jako walidację wyniku obliczeniowego wykonanego metodą analityczną.
Bibliografia
- P. Fotowicz: Nowe podejście w dziedzinie wyrażania niepewności pomiaru. PAR 7-8/2006.
- Guide to the Expression of Uncertainty in Measurement. ISO 1995.
- Evaluation of measurement data – Supplement 1 to the “Guide to the expression of uncertainty in measurement” – Propagation of distributions using a Monte Carlo method. JCGM 101:2008.
- P. Fotowicz: Obliczanie niepewności rozszerzonej metodą analityczną opartą na splocie rozkładów wielkości wejściowych. PAR 1/2005.
- P. Fotowicz, R. Jabłoński: Zastosowanie analitycznej metody obliczania przedziału rozszerzenia do oceny niepewności pomiaru małych średnic zewnętrznych laserowym przyrządem skanującym. PAR 2/2010.
dr inż. Paweł Fotowicz
Absolwent Politechniki Warszawskiej. Studia ukończył na Wydziale Mechaniki Precyzyjnej w 1981 r. Do 1999 r. pracował w Instytucie Metrologii i Systemów Pomiarowych PW, a od 1999 r. pracuje w Głównym Urzędzie Miar. Pracując na Politechnice Warszawskiej specjalizował się w dziedzinie laserowych technik pomiarowych, zajmując się konstrukcją przyrządów do bezstykowego pomiaru małych wymiarów zewnętrznych. Jest autorem sześciu patentów dotyczących konstrukcji tych przyrządów.
Pracując w Głównym Urzędzie Miar specjalizuje się w zagadnieniach teoretycznych metrologii, związanych z opracowaniem wyniku pomiaru, teorii błędu i niepewności pomiaru oraz terminologii metrologicznej. Prowadzi kursy szkoleniowe dotyczące praktyki obliczania niepewności pomiaru oraz wykłady dotyczącej tej problematyki. Jest autorem ponad stu publikacji w metrologicznych czasopismach krajowych i zagranicznych, m.in. takich jak „Measurement”, „Metrologia” czy „Measurement Science and Technology”. Jest międzynarodowym recenzentem czasopisma „Metrologia”, wydawanego pod egidą Międzynarodowego Biura Miar w Paryżu. Znajduje się na listach biograficznych: Who’sWho in the Word (USA), Who’sWho in Science and Engineering (USA) oraz International Biographical Centre (Cambridge, Anglia).
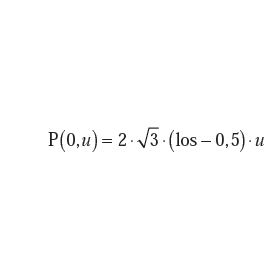
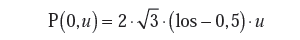
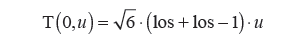
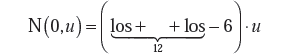
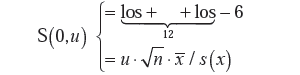
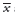
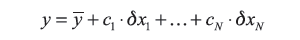
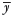
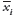
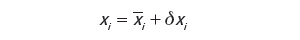
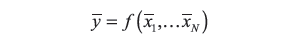
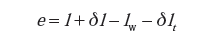
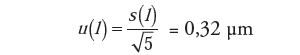
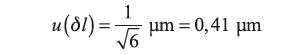
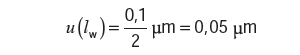
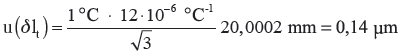
![Rys. 1. Widok strony obliczeniowej niepewności pomiaru metodą numeryczną [Worksheet of measurement uncertainty calculation by numerical method] Rys. 1. Widok strony obliczeniowej niepewności pomiaru metodą numeryczną [Worksheet of measurement uncertainty calculation by numerical method]](https://automatykaonline.pl/var/aol/storage/images/media/par/10_10/fotowicz/rys_1_300.png/76675-1-pol-PL/rys_1_300.png_medium.png)
![Rys. 2. Dystrybuanta numeryczna rozkładu wartości dla błędu wskazania wzorcowanego mikrometru [Distribution function attributed to the error of indication of calibrated micrometer] Rys. 2. Dystrybuanta numeryczna rozkładu wartości dla błędu wskazania wzorcowanego mikrometru [Distribution function attributed to the error of indication of calibrated micrometer]](https://automatykaonline.pl/var/aol/storage/images/media/par/10_10/fotowicz/rys2.png/76678-1-pol-PL/rys2.png_medium.png)
![Rys. 3. Histogram rozkładu wartości dla błędu wskazania wzorcowanego mikrometru [Histogram attributed to the error of indication of calibrated micrometer] Rys. 3. Histogram rozkładu wartości dla błędu wskazania wzorcowanego mikrometru [Histogram attributed to the error of indication of calibrated micrometer]](https://automatykaonline.pl/var/aol/storage/images/media/par/10_10/fotowicz/rys3.png/76681-1-pol-PL/rys3.png_medium.png)
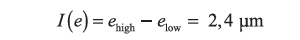
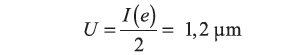
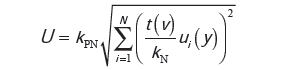
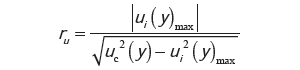
![Rys. 4. Widok strony obliczeniowej niepewności pomiaru metodą analityczną [Worksheet of measurement uncertainty calculation by analytical method] Rys. 4. Widok strony obliczeniowej niepewności pomiaru metodą analityczną [Worksheet of measurement uncertainty calculation by analytical method]](https://automatykaonline.pl/var/aol/storage/images/media/par/10_10/fotowicz/rys_4_300.png/76696-1-pol-PL/rys_4_300.png_medium.png)