Metoda symulacji procesów dynamicznych FINN – Excel 2007

Pierwotna forma tej metody symulacji była stosowana głównie do badań hydrauliki i termodynamiki sieci cieplnych. Stąd wywodzi się nazwa FINN (Flows IN Networks). FINN to jednolita i uniwersalna metoda komputerowej symulacji układów równań:

• algebraicznych liniowych i nieliniowych,
• różniczkowych zwyczajnych liniowych i nieliniowych,
• różnicowych liniowych (stałe opóźnienia) i nieliniowych (zmienne opóźnienia),
• mieszanych, złożonych z dowolnej kombinacji typów jw.

Uściślając, jest to numeryczna metoda uzyskiwania rozwiązań szczególnych ww. układów równań, która może być używana w każdej dziedzinie wiedzy technicznej czy przyrodniczej – wszędzie tam, gdzie badany proces można przedstawić w postaci modelu matematycznego opisanego układem równań z ww. listy.

Metoda była rozwijana i doskonalona w latach 70. i pierwszej połowie lat 80. ubiegłego wieku w Przemysłowym Instytucie Automatyki i Pomiarów PIAP przez zespół w składzie: Krystyna Judycka, Marzena Lipska-Bachtin, Barbara Omylińska, Stefan Frydliński, Jan Jabłkowski, Jerzy Miłosz i Andrzej Serwach. Niektóre rezultaty tych prac przedstawiono w artykułach [1–6]. W drugiej połowie lat 80. w Ośrodku Badawczo-Rozwojowym Ciepłownictwa przy SPEC autor stosował tę metodę do szeroko rozbudowanych badań automatyzacji procesów w systemach ciepłowniczych.

Oprogramowanie pierwotnej wersji FINN zostało napisane w języku FORTRAN 77. Dokumentacja tej wersji jest dostępna w formie elektronicznej [7] i może być przesłana przez autora na życzenie osób zainteresowanych (kontakt przez Redakcję PAR).

Niniejszy artykuł opisuje metodę FINN przystosowaną do wykonywania obliczeń za pomocą programu Excel 2007 [8]. Pakiet oprogramowania FINN – Excel 2007 pobrać można ze strony par.pl/finn [9]. Tutaj zamieszczono tylko opis podstawowych właściwości i możliwości tego pakietu.

Pętla czasowa

W modelach matematycznych procesów przejściowych (dynamicznych) występuje zawsze zmienna wiodąca procesu – czas. W przypadku rozwiązywania problemów dynamicznych na komputerach cyfrowych, zmienna wiodąca musi być zdyskretyzowana, tzn. kolejne stany procesu dynamicznego mogą być obliczane dla wybranych momentów czasu, różniących się od siebie o przyrost zwany krokiem całkowania. W przypadku rozwiązywania problemów statycznych, opisujących stany ustalone (niezależne od czasu), w metodzie FINN stosuje się w pętlach algebraicznych filtry dolnoprzepustowe, co faktycznie dynamizuje problem, wprowadzając sztucznie zmienną wiodącą, czyli umowny „czas”.

W rezultacie rozwiązywanie układów równań algebraicznych tą metodą sprowadza się do ich przekształcenia w równania różniczkowe zwyczajne. Należy podkreślić, że w odniesieniu do równań algebraicznych metoda zastępuje stosowane zazwyczaj metody iteracyjne. Różnica między zagadnieniem statycznym i dynamicznym formalnie sprowadza się do tego, że w pierwszym przypadku rozwiązaniem jest stan ustalony, a w drugim przebiegi w funkcji czasu (histogramy).

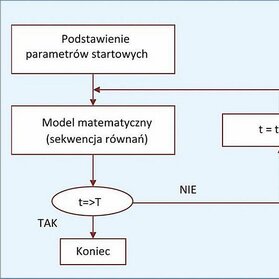
W obu porzypadkach wyniki metodą FINN – Excel 2007 uzyskuje się stosując tzw. pętlę czasową, wielokrotnie obliczając sekwencję równań modelu matematycznego, za każdym razem dla czasu większego o krok całkowania dt. W problemie statycznym rozwiązaniem jest wynik dla ostatniego kroku w pętli czasowej, natomiast w problemie dynamicznym rozwiązaniem jest zbiór wyników dla kolejnych kroków w pętli czasowej. Schemat blokowy sekwencyjnego algorytmu pętli czasowej pokazano na rys. 1.

Forma i porządek równań

Dla uniknięcia kłopotów i błędów równania opisujące model matematyczny dla danej chwili czasu t, tzn. równania wewnątrz pętli czasowej, powinny być zapisane w odpowiedniej formie i w odpowiedniej kolejności.

Przede wszystkim wszystkie równania powinny mieć postać kanoniczną – z lewej strony znaku równości zmienna zależna lub jej pierwsza pochodna względem czasu, a z prawej strony formuły ze zmiennymi niezależnymi i ewentualnie ze zmienną zależną (w przypadku występowania w modelu pętli sprzężenia zwrotnego). Równania różniczkowe zwyczajne wygodniej jest zapisywać w formie całkowej – z lewej strony zmienna zależna, nie jej pochodna, a z prawej strony całka ze stosownej formuły. Równania różnicowe powinny mieć postać: z lewej strony zmienna zależna, a z prawej formuła opóźniająca zmienną niezależną.

Oczywiście w powyższych wywodach termin „zmienna niezależna” należy odnieść do danego równania, bowiem z istoty metody wynika, że wszystkie zmienne procesu są zależne od czasu, czyli od zmiennej wiodącej, kontrolującej sekwencję zdarzeń (kolejnych wyników obliczeń). Porządek równań powinien odpowiadać strukturze modelu matematycznego, który z kolei odzwierciedla strukturę opisywanego obiektu fizycznego.

W problemach statycznych na początku sekwencji należy zapisywać równania z filtrami, czyli zbiór równań różniczkowych w postaci całkowej. Następnie wynikającą ze struktury modelu sekwencję powiązań między zmiennymi filtrowanymi i dalej wynikającą ze struktury modelu sekwencję powiązań między zmiennymi niefiltrowanymi.

W problemach dynamicznych na początku pętli należy umieszczać równania opisujące tzw. model wymuszeń, czyli przebiegi czasowe zmiennych zewnętrznych (sterujących i zakłócających) w stosunku do struktury modelu. Dalsza kolejność równań powinna odpowiadać strukturze powiązań wewnętrznych modelu, czyli tzw. przyczynowości.

Warunki początkowe

Skoro cała metoda polega na traktowaniu każdej symulacji jako procesu dynamicznego (rzeczywistego lub sztucznego), to zawsze pojawia się problem ustawienia na wejściu do pętli warunków początkowych dla zmiennych wyjściowych z procedur historycznych. W przypadku rozwiązywania problemu statycznego wartości tych warunków początkowych mogą być dowolne (np. zerowe). Lepiej jednak zadeklarować jako początkowe wartości co prawda dowolne, ale nie różniące się więcej niż o rząd od spodziewanych wyników.

Poważniejszy jest problem podstawienia właściwych wartości warunków początkowych przy symulacji dynamicznego procesu rzeczywistego. W tym przypadku błędna wartość warunku początkowego jest de facto dodatkowym skokowym zakłóceniem w chwili t = 0. Takie zakłócenie fałszuje wynik obliczeń przynajmniej w pierwszych krokach.

Skutecznym sposobem doboru prawidłowych warunków początkowych jest dwuetapowy rozruch programu symulacyjnego. W pierwszym etapie wstawia się dowolne, aczkolwiek rozsądnie wybrane warunki początkowe. W kolumnach zawierających przebiegi zewnętrznych funkcji wymuszających we wszystkich komórkach każdej kolumny wstawia się wartość wymuszenia w zerowej chwili czasu i rozpoczyna się symulację. Wartości odpowiednich zmiennych w stanie ustalonym, czyli w ostatnim kroku pętli czasowej, są właściwymi warunkami początkowymi. W drugim etapie te warunki początkowe wstawia się do funkcji z historią, natomiast w kolumny z wymuszeniami zewnętrznymi wstawia się właściwe czasowe przebiegi funkcji wejściowych i ponownie uruchamia symulację. Wówczas proces przejściowy jest wymuszany wyłącznie przez te wejścia, a nie przez źle dobrane warunki początkowe.

Bardziej skomplikowany jest przypadek doboru warunków początkowych w modelu złożonym z równań różnicowych z opóźnieniami czasowymi. Wynika to stąd, że procedury opóźniające są skonstruowane tak, że przez czas równy bądź mniejszy opóźnieniu transportowemu wydają na wyjściu wartość warunku początkowego. W pakiecie [9] w drugim przykładzie symulacji jest opisany i zastosowany skuteczny sposób rozwiązania problemu. Symulacja dotyczy badania przebiegów temperatury zasilania sieci cieplnej w okresie jednej doby. Problem rozwiązano, stosując „lotny start”. Symulacja zaczyna się z trzygodzinnym wyprzedzeniem (ostatnie trzy godziny poprzedniej doby), natomiast przebiegi badane i oceniane wskaźnikami jakości są mierzone według drugiej osi czasu, rozpoczynającej się trzy godziny po starcie symulacji od godziny „zerowej”. Trzygodzinne przesunięcie między osiami czasu wybrano tak, aby w chwili początkowej dla przebiegów badanych i ocenianych na wyjściu każdej funkcji opóźniającej znajdowały się rzeczywiste wartości opóźniane, a nie warunki początkowe. Trzy godziny to czas dłuższy niż suma wszystkich opóźnień transportowych w najdłuższej magistrali.

Przystosowanie metody FINN do programu Excel 2007

Zdecydowana większość użytkowanych obecnie komputerów osobistych jest wyposażona w pakiet Microsoft Office, którego częścią jest arkusz kalkulacyjny Excel. Ten program to potężne narzędzie do obliczeń numerycznych, zwłaszcza wersja Excel 2007. W praktyce możliwości obliczeniowe Excela są wykorzystywane w śladowej postaci, nie zmienia to jednak faktu, że dzięki Excelowi każdy użytkownik komputera osobistego może „domowym sposobem” wykonywać m.in. złożone symulacje procesów dynamicznych. Trzeba tylko dostosować metodę FINN do właściwości arkusza kalkulacyjnego.

Excel to gigantyczny arkusz kalkulacyjny. Każdy arkusz w skoroszycie Excel 2007 to tablica składająca się z 1 048 576 wierszy i 16 384 kolumn, co w sumie daje ponad 17 miliardów komórek. Zasadniczą różnicą między programem napisanym w języku FORTRAN lub pokrewnych a aplikacją napisaną w programie Excel jest to, że w drugim przypadku wszystkie dane z wszystkich kroków symulacji są dostępne i wyświetlane w komórkach. Dlatego m.in. nie trzeba deklarować specjalnych komórek do pamiętania danych z poprzednich kroków symulacji. Wystarczy odwołanie do odpowiednich istniejących adresów z przeszłości względem zmiennej wiodącej.

Pomysł, jak adaptować pętlę czasową FINN do arkusza kalkulacyjnego okazał się prosty. Otóż poszczególne kroki w pętli czasowej to kolejne wiersze arkusza. Natomiast poszczególne komórki każdego wiersza (kolejne kolumny arkusza) to sekwencja instrukcji wewnątrz pętli, opisujących model matematyczny symulowanego procesu. Zatem wystarczy w wierszu przypisanym do pierwszego kroku symulacji wpisać sekwencję instrukcji obliczeniowych opisujących model procesu i następnie skopiować ten wiersz w dół arkusza tyle razy, ile kroków powinna mieć pętla czasowa. Następnie zostaną wykonane obliczenia symulacyjne (czasem trwające wiele minut!).

1. Skoroszyt należy zapisać w formacie pliku opartym na kodzie XML i z obsługą makr.
2. W skoroszycie nie wolno włączać obliczeń iteracyjnych. Obliczenia symulacyjne są bardzo złożone, ale wykonywane w rytmie stałego kroku całkowania. Wbudowana w Excel procedura iteracyjna na pewno zakłóci ten rytm. Ponadto, brak włączonej obsługi zależności uwikłanych między zmiennymi wygeneruje ostrzeżenie o odwołaniu cyklicznym, co jest dla użytkownika sygnałem, że nie dostrzegł pętli algebraicznej w swoim algorytmie. Jeżeli ta pętla musi tam być, należy ją przerwać, odwołując się do wartości zmiennej uwikłanej z poprzedniego kroku symulacji, a nie z bieżącego. Wtedy ostrzeżenie o odwołaniu cyklicznym zniknie i można kontynuować programowanie. Co więcej, jeżeli wykryta pętla jest pętlą algebraiczną, należy włączyć filtr dolnoprzepustowy, dynamizując ją sztucznie.
3. Z powodu konieczności odwołań do wartości zmiennych z poprzedniego kroku, w arkuszu symulacyjnym musi być pozostawiony wolny wiersz między wierszem nagłówków i wierszem pierwszego kroku symulacji. W tym wierszu, w razie potrzeby, zapisuje się wartości zmiennej z „minusowego” kroku symulacji.
4. Skoroszyt symulacyjny powinien zawierać co najmniej trzy arkusze: Dane, Symulacja i Wykresy. W arkuszu Dane zaleca się umieszczać wszelkie parametry algorytmu symulacji np. krok całkowania dt. Można dowolnie definiować nazwy przypisane zarówno do komórek z danymi, jak i do całych tablic z danymi (stałe tablicowe). W tym celu należy korzystać z zakładki Formuły/Nazwy zdefiniowane. Arkusz Symulacja jest głównym arkuszem, w którym realizowana jest pętla czasowa. Dwie pierwsze kolumny powinny być zarezerwowane dla licznika kroków i dla zmiennej wiodącej procesu dynamicznego, czyli czasu. Trzeci arkusz Wykresy to arkusz do przechowywania wyników symulacji, zwykle w formie wykresów. Wyniki symulacji z arkusza głównego powinny być kopiowane do arkusza Wykresy z użyciem opcji Wklej wartości. Dzięki temu kolejne wyniki symulacji będą trwale zachowane w arkuszu z wynikami.
5. Ze względu na konieczność posługiwania się w trakcie symulacji funkcjami specjalnymi FINN – Excel 2007, w skoroszycie symulacyjnym powinna być uaktywniona zakładka Deweloper, normalnie ukryta.

Funkcje specjalne FINN – Excel 2007

W tej metodzie, jak zresztą w każdej innej, występują powtarzające się procedury o charakterze czysto matematycznym (ogólne), jak również związane z konkretnymi zastosowaniami (specjalistyczne). Te procedury można podzielić na „historyczne” i „bez historii”, czyli na zależne od zmiennej wiodącej (ściśle od stanu/ów) w przeszłych momentach) oraz niezależne od czasu.

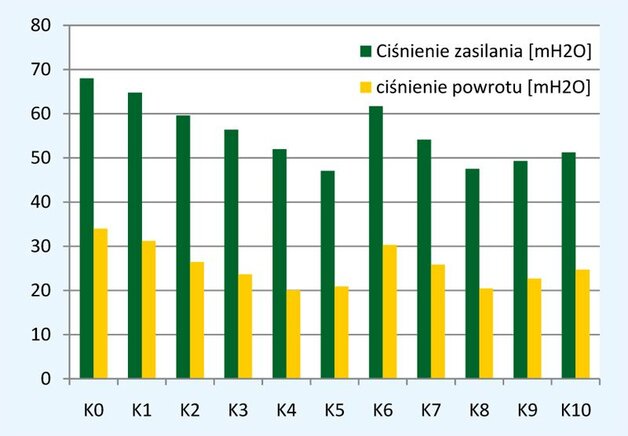
Przykład 1. Obliczanie rozkładu ciśnień w komorach magistralnych sieci cieplnej – rozwiązanie szczególne układu algebraicznych równań nieliniowych. Przykładowe wyniki symulacji pokazano na rys. 2.

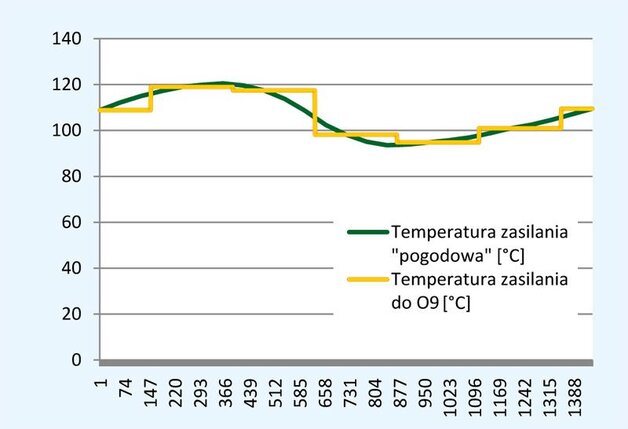
Przykład 2. Badanie algorytmów sterowania temperaturą zasilania sieci cieplnej – rozwiązanie szczególne układu równań różnicowych względem czasu. Celem badań był wybór najdokładniejszego sposobu sterowania ze źródła temperaturą zasilania sieci cieplnej w funkcji temperatury zewnętrznej. Na rys. 3 pokazano przykładowe przebiegi czasowe temperatury zasilania w komorze na końcówce sieci dla optymalnego sterowania z antycypacją wg prognozowanej temperatury zewnętrznej w porównaniu do przebiegów idealnych, czyli zależnych ściśle od pogody.

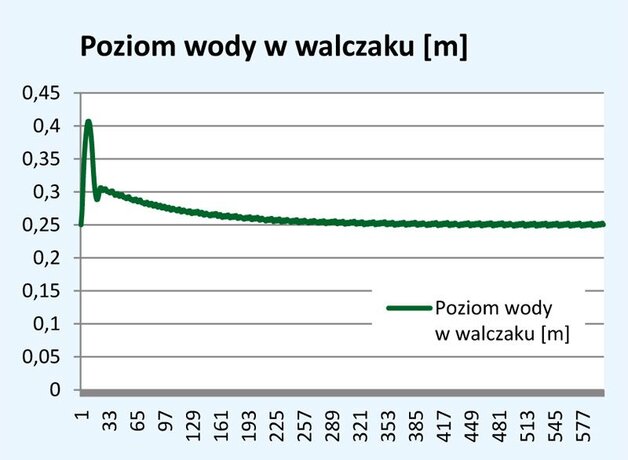
Przykład 3. Automatyczna regulacja poziomu wody w walczaku kotła parowego – rozwiązanie szczególne układu nieliniowych równań różniczkowych względem czasu. Celem symulacji był dobór optymalnych (dla minimum wskaźnika jakości) nastaw dynamicznych regulatora PI. Optymalną odpowiedź przejściową układu regulacji na skokowy wzrost rozbioru pary pokazano na rys. 4.

Procedury bez historii są to typowe funkcje jednej lub wielu zmiennych. Mogą mieć postać analityczną lub tabelaryczną. W drugim przypadku są to procedury interpolacyjne.

Procedury historyczne można podzielić na dwie grupy:

• zależne od czasu bieżącego i wartości zmiennych wejściowych dla czasu o krok do tyłu,
• zależne od czasu bieżącego i zbioru wartości zmiennych wejściowych z przeszłości, tzn. w chwilach – dt, –2*dt, …, –n*dt.

Do tych pierwszych, wykorzystujących informację o krok do tyłu, należy w sposób oczywisty całkowanie, ale także w sposób mniej oczywisty różniczkowanie oraz histereza. Procedury, w których trzeba zapamiętywać dane z wielu kroków do tyłu to opóźnienie transportowe stałe i zmienne.

W pakiecie [9] w skoroszycie Startowy.xlsm są umieszczone funkcje specjalne zdefiniowane przez autora. Są udostępnione podobnie jak funkcje standardowe. Tych funkcji jest osiemnaście. Dostęp do ich postaci źródłowej jest możliwy w edytorze VBA w zakładce Deweloper. Ponadto w arkuszu Dane umieszczono listę nazw funkcji specjalnych z komentarzami, opisami składni funkcji i znaczenia jej argumentów. Te komentarze ułatwiają programowanie aplikacji symulacyjnej, bez konieczności sięgania do kodu źródłowego zdefiniowanych funkcji specjalnych. W razie konieczności użytkownik sam może zdefiniować potrzebną mu funkcję specjalną korzystając z edytora VBA.

Zastosowania symulacji metodą FINN

Współtwórcy metody FINN w jej pierwotnej postaci stosowali ją do symulacji różnorodnych obiektów, w większości z dziedziny techniki. Oto lista tych zastosowań:

• dynamika serwomechanizmów elektrohydraulicznych w napędach obrabiarek,
• dynamika napędów hydraulicznych maszyn roboczych,
• projektowanie i zastosowania regulatorów bezpośredniego działania,
• dynamika układów automatycznej regulacji w węzłach cieplnych i kotłowniach przemysłowych,
• hydraulika sieci cieplnych oraz dynamika transportu ciepła w tych sieciach,
• dynamika układu krwionośnego człowieka – prace wstępne w programie budowy sztucznego serca.

Zastosowanie zmodyfikowanej metody FINN – Excel 2007 zilustrowano trzema przykładami [9]. Wszystkie pochodzą z branży energetyki cieplnej. Daje to gwarancję poprawności stosowanych modeli matematycznych i nie umniejsza uniwersalności metody, bowiem przykłady dobrano tak, aby pokazać jej różnorodne możliwości.

Podsumowanie

Oddawany użytkownikom do eksploatacji pakiet FINN – Excel 2007 [9] jest mocnym i wygodnym narzędziem symulacji procesów dynamicznych. Może być zastosowany na każdym komputerze osobistym wyposażonym w standardowy pakiet Microsoft Office 2007. Trzeba jednak pamiętać, że jest to tylko narzędzie. O sukcesie badań symulacyjnych decyduje przede wszystkim poprawność użytego modelu matematycznego i dobrze zaprojektowany plan badań.

Wyróżnia się dwa typy modeli matematycznych (plus oczywiście modele mieszane):

• fenomenologiczne – budowane z użyciem wprost równań opisujących prawa fizyki,
• opisowe – powstające na zasadzie analizy zachowań „czarnej skrzynki”.

W technice dominują modele fenomenologiczne. Natomiast w naukach przyrodniczych praktycznie wyłącznie trzeba posługiwać się modelami opisowymi. Dodatkowym problemem jest to, że FINN – Excel 2007 służy do symulacji modeli deterministycznych. Natomiast badania przyrodnicze są z reguły opracowywane za pomocą metod statystycznych. Wyjściem z kłopotu jest potraktowanie wartości oczekiwanych, pozyskiwanych ze statystycznej obróbki eksperymentów jako parametrów deterministycznego modelu opisowego, budowanego dla celów symulacji.

Z wieloletniego doświadczenia autora płynie przekonanie, że najlepsze wyniki w badaniach symulacyjnych daje współpraca zespołowa specjalisty od symulowanego procesu ze specjalistą od symulacji komputerowej.

Ostatnia uwaga dotyczy wyglądu arkuszy symulacyjnych. Można w tym celu wykorzystać ogromne bogactwo możliwości jakie daje Excel 2007. Okna dialogowe, kontrolki, ukrywanie wybranych wierszy i kolumn, obramowanie, kolorowanie itd. W zamieszczonych przykładach z premedytacją nie stosowano takich chwytów. Symulacja komputerowa to rodzaj warsztatu badawczego, który nie musi być ładny, lecz wygodny, skuteczny i podatny na szybkie przeróbki. Dlatego należy ograniczać wysiłki zmierzające do upiększania arkusza symulacyjnego. Nie dotyczy to rzecz jasna wyników badań przygotowywanych do publikacji.

Bibliografia

1. Serwach A., Frydliński S., Omylińska B., Komputerowa symulacja dynamiki cieczowego wymiennika ciepła, Biuletyn MERA-PIAP, nr 5/1980 (85).
2. Serwach A., Frydliński S., Symulacja przepływów w sieciach, Biuletyn MERA-PIAP, nr 2/1981 (88).
3. Serwach A., Frydliński S., Omylińska B., Niektóre problemy automatycznej regulacji temperatury w wymiennikach ciepła, Biuletyn MERA-PIAP, nr 3/1981 (89).
4. Serwach A., Miłosz J., Komputerowa symulacja sieci cieplnych (metoda i zasady użytkowania), Biuletyn MERA-PIAP, nr 5-6/1983 (100-101).
5. Serwach A., Model statyczny cieczowego wymiennika ciepła, Biuletyn MERA-PIAP, nr 1/1984 (102).
6. Miłosz J., Procedura interpolacji liniowej funkcji dwóch zmiennych, Biuletyn MERA-PIAP, nr 3/1985 (110).
7. Serwach A., Dokumentacja FINN – FORTRAN 77, zbiory własne autora.
8. Walkenbach J., Excel 2007 PL. Biblia. Wiedza obiecana, Wydawnictwo Helion, 2007.
9. Pakiet oprogramowania FINN – Excel 2007, [par.pl/finn], 2011

dr inż. Andrzej Serwach