Zastosowanie metod sztucznej inteligencji w energetyce
Anna Ściążko - AGH print
Metody sztucznej inteligencji są stosowane w modelowaniu, przewidywaniu, planowaniu (optymalizacji) i kontroli procesów. W artykule pokazano typowe przykłady użycia sztucznej inteligencji, charakterystyczne dla każdej z grup. Przedstawiono także możliwe przyszłe wykorzystania tego typu metodologii, w szczególności w inteligentnych systemach elektroenergetycznych – Smart Grid. Artykuł przedstawia i omawia przykład wykorzystania sztucznej inteligencji w modelowaniu systemu elektroenergetycznego, złożonego z takich elementów: elektrociepłownia geotermalna, źródło geotermalne, miejska sieć ciepłownicza oraz zakład przemysłowy. Zadanie polegało na przygotowaniu modelu komputerowego rozważanego systemu oraz wielokryterialnej optymalizacji problemu. Jakość każdego z rozwiązań była oceniana na podstawie dwóch różnych funkcji dopasowania: obliczonej wartości kosztów inwestycyjnych oraz sprawności egzergetycznej systemu. Pokazano w jaki sposób można wykorzystać genetyczny algorytm optymalizacji wielokryterialnej oraz modelowanie zastępcze z wykorzystaniem sztucznej sieci neuronowej do analizy zadanego problemu. Rezultaty optymalizacji zostały zobrazowane na diagramie Pareto, na ich podstawie pokazano kilka typów możliwych rozwiązań projektowych (niewielkie koszty inwestycyjne i niska sprawność, wysokie koszty inwestycyjne ale wysoka sprawność oraz rozwiązanie pośrednie). Dla modelu zastępczego określono jego dokładność oraz dopasowanie do oczekiwanych rezultatów.
Jedną z największych zalet metod informatycznych nazywanych metodami sztucznej inteligencji jest ich zdolność do rozwiązywania skomplikowanych problemów, które dodatkowo są słabo zdefiniowane oraz potencjalnie obarczone dużymi błędami. Tradycyjne algorytmy zazwyczaj nie radzą sobie z tego typu zadaniami, bądź ich czas działania jest bardzo długi. Metody sztucznej inteligencji, które często są algorytmami heurystycznymi, nie gwarantują uzyskania pozytywnego rezultatu, jednak bardzo często dają na tyle dokładne i szybkie wyniki, że są najlepszym sposobem rozwiązania problemu. Ich generalne cechy to zdolność do nauki na podstawie przykładów (np. danych badawczych), łatwość w generalizacji cech problemu i wychwytywanie wzorców w problemach nieliniowych oraz umiejętność radzenia sobie z szumami, zakłóceniami i niekompletnością danych wejściowych. Kolejną zaletą metod sztucznej inteligencji jest to, że model raz przygotowany i nauczony, przeprowadza kolejne symulacje i predykcje bardzo szybko.
Sztuczna inteligencja może być wykorzystywana w energetyce do trzech różnych typów problemów: modelowania, przewidywania i planowania (optymalizacji) oraz do kontroli procesów.
Modelowanie
W dzisiejszym świecie najcenniejsze są wiedza oraz czas. Modelowanie komputerowe pozwala uzyskać wiedzę o skomplikowanych systemach i urządzeniach energetycznych w stosunkowo krótkim czasie. Jest ono szczególnie istotne w kontekście optymalizacji procesów, gdy wykonujemy setki obliczeń dla jednego przypadku (budowanie rzeczywistych modeli dla każdego z wariantów rozwiązania byłoby niemożliwe z przyczyn technicznych). Modele tego typu sąwykorzystywane w każdej z dziedzin energetyki, począwszy od symulacji pojedynczych urządzeń, przez projekty układów elektroenergetycznych, takich jak elektrownie, do modeli technicznych, politycznych i społecznych całych systemów energetycznych dla regionu czy kraju.
Modele systemów energetycznych są zwykle tworzone jako olbrzymie układy równań różniczkowych opisujących zachowanie danego systemu. Takie rozwiązania są bardzo czasochłonne oraz często wymagają wprowadzenia uproszczeń. Czasem nie jest znana dokładna natura problemu, o którym wiedzę czerpiemy jedynie z obserwacji, bądź wykorzystywane oprogramowanie narzuca określony sposób modelowania, który nie pozwala na wierne odtworzenie wszystkich niuansów rozważanego systemu.
Alternatywnym rozwiązaniem, które może zostać zastosowane w takiej sytuacji, jest wykorzystanie sztucznej sieci neuronowej jako modelu zastępczego. Sieć neuronowa jest uczona oryginalnymi danymi obserwacyjnymi (gdy są dostępne) bądź przykładami wygenerowanymi przez przygotowany wcześniej tradycyjny model (w przypadku, kiedy głównym celem jest przyspieszenie działania), np. w procesie optymalizacyjnym. W takim przypadku pojawia się możliwość stworzenia ciekawego systemu hybrydowego: połączenia modelu zastępczego opartego na sztucznej sieci neuronowej z genetycznym algorytmem optymalizacyjnym [10]. Idea takiego połączenia jest następująca: najpierw tworzymy model zastępczy (sieć neuronową) oparty na losowo wygenerowanych punktach z całej przestrzeni potencjalnych rozwiązań. Następnie przeprowadzamy zadaną liczbę iteracji algorytmu optymalizacyjnego. W kolejnym kroku douczamy sieć neuronową punktami z aktualnej populacji algorytmu genetycznego. Tak przygotowany model zastępczy jest wykorzystywany w kolejnych iteracjach optymalizacyjnych.
Podana procedura jest przeprowadzana aż do uzyskania zadawalającego rezultatu optymalizacyjnego. Należy zauważyć, że tworzona w ten sposób sieć neuronowa jest bardzo dokładna w najbardziej istotnych podprzestrzeniach(dających dobre rezultaty w optymalizacji), ponieważ w jej uczeniu wykorzystano najwięcej przykładów z tych obszarów.
Przewidywanie i optymalizacja
Najwięcej praktycznych zastosowań metod sztucznej inteligencji w energetyce pojawiających się w opracowaniach naukowych dotyczy możliwości ich wykorzystywania do przewidywania oraz optymalizacji.
Bardzo popularne są próby aproksymacji i przybliżania kształtu wykresu zapotrzebowania na energię elektryczną. Badania takie są prowadzone nie tylko przez energetyków, ale także przez informatyków oraz osoby zajmujące się teoretycznym rozwojem różnych metod sztucznej inteligencji. Wyjaśnienie tego faktu jest bardzo proste – dane dotyczące zapotrzebowania na energię elektryczną są ogólnie dostępne oraz przygotowane w łatwo przetwarzalnym formacie. Ponadto popyt na energię jest zależny od bardzo wielu czynników (dzień tygodnia, pogoda, pora dnia, pora roku). Powstające w ten sposób szeregi czasowe są idealne do testowania różnych rozwiązań, jak typowe sieci neuronowe [1], sieci Kohonena [7] czy maszyny wektorów nośnych [3]. Jednocześnie określenie przyszłego zapotrzebowania na energię, zarówno w perspektywie krótkoterminowej, jak i długoterminowej, jest bardzo ważne w kontekście jej produkcji i sprzedaży. Takie dane mogą być wykorzystywane przy zawieraniu kontraktów na dostawę energii, tworzeniu planów produkcyjnych czy w ustalaniu planów taryfowych.
Podobny sposób wykorzystania sztucznej inteligencji dotyczy przewidywania pogody – szczególnie nasłonecznienia oraz siły wiatru [6]. Takie prognozy znajdują zastosowanie przy planowaniu systemów energetycznych opartych na odnawialnych źródłach energii, które silnie zależą od niedeterministycznych zachowań natury. W literaturze można znaleźć wiele przykładów tego typu badań, co jest związane z dostępnością danych oraz typowością rozwiązania (przewidywanie szeregów czasowych to jedno z podstawowych zastosowań sieci neuronowych). Kolejnym przykładem zastosowania sieci neuronowych w energetyce są próby przewidywania energochłonności budynków [6].
Mniej oczywistym, ale równie ważnym zastosowaniem tych metod jest planowanie budowy systemów elektroenergetycznych – dobieranie odpowiednich generatorów (na przykład różnych źródeł odnawialnych w kontekście mikrogeneracji)oraz tworzenie i lokalizacja elementów sieci przesyłowej. Tego typu rozwiązania mogą wykorzystywać na przykład logikę rozmytą [5]. Kolejną korzyścią, którą można czerpać z zastosowania metod sztucznej inteligencji w energetyce jest nowoczesne i innowacyjne podejście do projektowania podzespołów. Odpowiednio zbudowany algorytm może pomóc w doborze parametrów rozważanego projektu [9]. Inne podejście to zastosowanie systemów ekspertowych we wspomaganiu decyzji projektowych.
Sztuczną inteligencję można także stosować w problemach, które są zwykle rozwiązywane w sposób numeryczny za pomocą symulacji komputerowych. Przykładami tego typu problematyki mogą być próby modelowania procesu rozchodzenia się ciepła w różnego typu elementach (dla których tradycyjne metody obliczeniowe nie są odpowiednio wydajne) czy analizy dotyczące rozchodzenia się turbulencji w przepływach cieczy.
Kontrola procesów
Sztuczna inteligencja zdaje rezultaty także w przypadku wprowadzenia jej do systemów kontroli procesów. Wspomniane wcześniej próby przewidywania zapotrzebowania na energię elektryczną mogą być wykorzystywane w sterowaniu elementami systemu generacyjnego oraz w algorytmie do ustalania kontraktów na zakup energii elektrycznej.
Interesującym pomysłem jest wykorzystanie systemu wieloagentowego do kontroli energetycznego systemu hybrydowego (składającego się z różnych źródeł generacji energii elektrycznej, w większości opartych na energii odnawialnej) [4]. Każdy z generatorów i magazynów energii oraz każde z zapotrzebowań na energię są reprezentowane jako pojedynczy agent. Agent ma ograniczoną świadomość środowiska (wie, co jest dla niego dobre, jednak nie ma wiedzy o całym systemie). Agenty komunikują się ze sobą i współpracując podejmują autonomiczne decyzje. Tutaj odpowiedzialność jest rozdzielona na poszczególne agenty – jest to system analogiczny do roju mrówek, gdzie każdy organizm ma swoje zadania. Okazuje się, że tak zaprojektowany system kontroli może zminimalizować straty energii w systemie energetycznym.
Metody sztucznej inteligencji mogą być ponadto wykorzystywane do odczytu oraz kontroli parametrów środowiska, takich jak temperatura czy wilgotność. Sprawiają one, że system jest w stanie rozpoznać i zareagować odpowiednio szybko na dynamiczne zmiany otoczenia.
Smart Grid
Jednym z obiecujących kierunków rozwoju metod sztucznej inteligencji w problematyce dotyczącej rozwoju energetyki są inteligentne systemy elektroenergetyczne – Smart Grid. Już w samej ich definicji widać analogie i powiązania z metodami wieloagentowymi czy sieciami neuronowymi.
Idea sieci Smart Grid bazuje na koncepcji ulepszenia standardowej sieci elektroenergetycznej. Obecnie systemy takie składają się z kilku dużych generatorów energii, która jest dostarczana za pomocą sieci przesyłowej do wielu odbiorców. Głównymi problemami są tu olbrzymie straty energii podczas jej przesyłu na duże odległości, duże dysproporcje między poborem mocy w godzinach szczytu oraz normalnego użytkowania i niezdolność do szybkich reakcji sieci na nieprzewidziane sytuacje. Smart Grid zapewni komunikację między wszystkimi elementami ulepszonej sieci elektroenergetycznej, wprowadzi niewielkie źródła energii (w szczególności mikrogeneratory energii odnawialnej) oraz pozwoli na wygładzenie krzywej zapotrzebowania na energię elektryczną. Podejście takie pozwoli zwiększyć efektywność dostarczania energii oraz zmniejszyć koszty, jednak wymaga ono kompleksowego planu i zarządzania oraz zmian we wszystkich elementach sieci.
Wiele z omówionych zastosowań metod sztucznej inteligencji może zostać wykorzystanych przy projekcie nowoczesnej Smart Grid. Oprócz „standardowych”zastosowań(jak przewidywanie zapotrzebowania, warunki pogodowe czy kontrola i zarządzanie produkcją) warto wspomnieć o możliwości wykorzystania sztucznej inteligencji po stronie odbiorców końcowych energii. Aby wykorzystywać efektywnie, energię najlepiej jest, gdy zapotrzebowanie osiąga podobny poziom całą dobę. Pomóc może w tym odpowiedni, zarządzany przez sztuczną inteligencję, system kontroli ładowania i rozładowania urządzeń w domach i biurach. Urządzenia mogłyby być ładowane w czasie, gdy ogólne zapotrzebowanie na energię jest niewielkie (bądź ładowane na przemian czy w odpowiedniej kolejności według priorytetów). Należy wziąć pod uwagę zapotrzebowanie na różnego typu usługi – takie wzorce mogłyby być wychwytywane przez odpowiednio nauczone sieci neuronowe. Ciekawym konceptem jest także włączenie do sieci samochodów elektrycznych, które mogą być rozważane jako swoiste magazyny energii na kółkach.
Analiza złożonego systemu energetycznego
Przykładem zastosowania omówionych metod sztucznej inteligencji jest analiza złożonego systemu elektroenergetycznego (rys. 1). Badany system został zaprojektowany oraz zamodelowany komputerowo, a następnie wykorzystany do przeprowadzenia optymalizacji (wykorzystanie algorytmu genetycznego) i na jego podstawie przygotowano model zastępczy (oparty na sieci neuronowej).
W jego skład wchodzą elementy takie jak elektrociepłownia geotermalna, miejska sieć ciepłownicza, zakład przemysłowy (mleczarnia) oraz sieć elektroenergetyczna. Schemat systemu oprócz jego ogólnych elementów pokazuje także główne założenia dotyczące poszczególnych podsystemów. Najważniejszymi informacjami, są dane o temperaturach charakterystycznych dla różnych strumieni. Drugim ważnym założeniem jest to, iż cała energia, która nie jest wykorzystywana bezpośrednio do zaspokojenia potrzeb miejskiej sieci ciepłowniczej oraz mleczarni, służy do wytwarzania prądu elektrycznego, który następnie jest sprzedawany do sieci.
Na podstawie przyjętych założeń, można obliczyć ilość ciepła dostępną w systemie. Maksymalna moc cieplna, dostarczane przez źródło geotermalne wynosi:
Zapotrzebowanie cieplne w systemie jest sumą zapotrzebowań miejskiej sieci ciepłowniczej (14 MW) oraz mleczarni. Zapotrzebowanie cieplne mleczarni jest wyznaczane na podstawie analizy Pinch Point Technology procesu technologicznego. Poszczególne etapy wytwarzania produktów końcowych wymagają dostarczenia bądź odbioru ciepła. Za pomocą odpowiednio umieszczonych wymienników ciepła jesteśmy w stanie zminimalizować zapotrzebowanie na zewnętrzne chłodzenie oraz ogrzewanie. W analizie założono, że mleczarnia wykorzystuje jedynie niezbędną jej moc cieplną, zapewnianą przez elektrociepłownię geotermalną. W wyniku analizy Pinch Point ustalono, że moc ta wynosi 320 kW, a zakres temperatur wynosi od 58 °C do 98 °C.
Najważniejszym elementem systemu jest elektrociepłownia geotermalna. Założono, że jest ona zbudowana na podstawie cyklu ORC (Organic Rankine Cycle). Schemat tego cyklu został pokazany na rys. 2. Graf ten został wykorzystany do przygotowania modelu komputerowego elektrociepłowni w programie VALI. Program ten wykorzystuje iteracyjny algorytm rozwiązywania dużych układów równań, opisujących poszczególne elementy systemu.
Następny krok dotyczył przygotowania modelu całego problemu, to znaczy połączenia wszystkich części: elektrociepłowni, mleczarni oraz sieci ciepłowniczej i elektroenergetycznej. Model komputerowy został przygotowany w programie OSMOSE. Program OSMOSE oraz program EIAMPL (wykorzystywany do integracji wszystkich strumieni energetycznych) są oprogramowaniem rozwijanym na Politechnice w Lozannie (EPFL). Program OSMOSE pozwala zarówno na pojedynczą ewaluację systemu (wraz z przygotowaniem analizy poszczególnych strumieni ciepła), jak i na przeprowadzenie optymalizacji wielokryterialnej dla danego problemu. Optymalizacja taka jest przeprowadzana za pomocą algorytmu genetycznego, gdzie losowe zbiory parametrów wejściowych tworzą populację początkową, a przygotowany model systemu służy do obliczenia wartości funkcji dopasowania.
Dla przedstawionego problemu można wybrać wiele różnych funkcji oceny jego jakości. Wskaźniki te mogą zostać podzielone na trzy zasadnicze grupy: wskaźniki i nansowe, środowiskowe oraz termodynamiczne. Skoncentrujemy się na dwóch przykładowych funkcjach oceny: sprawności egzergetycznej systemu oraz kosztach inwestycyjnych. W skład kosztów inwestycyjnych wchodzi wiele czynników. Zakładamy, że koszty systemu dotyczą jedynie kosztów wybudowania elektrociepłowni oraz kosztów odwiertów geotermalnych. Ogólny wzór, który wykorzystano w obliczeniach ma postać:
gdzie: Kturbiny – całkowity koszt zainstalowanych turbin; Kpompy – całkowity koszt zainstalowanych pomp; Kwymienniki_ciepła – koszt zainstalowanych wymienników ciepła; Kodwiert – koszt wykonania odwiertu geotermalnego; FI [%]– współczynnik inwestycji.
Koszty wykonania odwiertu określa wzór:
gdzie: z [m] – głębokość odwiertu, n – liczba odwiertów.
Dla przygotowanego modelu założono, że zostały wykonane dwa odwierty geotermalne, każdy o głębokości 1200 m. Dwa odwierty zapewniają pożądane warunki przepływu czynnika. Ponadto założono wartość współczynnika inwestycji FI = 20 %. Współczynnik ten zakłada pokrycie kosztów przeznaczonych na dodatkowe, niewymienione wcześniej elementy systemu. Pokrywa on także koszty pracy potrzebnej do zbudowania poszczególnych elementów. Drugi brany pod uwagę wskaźnik jakości systemu to jego sprawność egzergetyczna. Wskaźnik ten wyznacza efektywność procesu w kontekście drugiej zasady termodynamiki. Jest to wskaźnik, który bierze pod uwagę temperatury procesów jak i temperaturę otoczenia. Wartość ta mówi o stosunku sprawności rzeczywistej do największej teoretycznej możliwej do uzyskania.
| gdzie: | – egzergia, |
| – przepływ ciepła dla miejskiej sieci grzewczej: |
Qmleczarnia [kW] – przepływ ciepła dla mleczarni
Qgeotermia[kW] – teoretyczny przepływ ciepła ze źródła geotermalnego
Oprócz wybrania odpowiednich funkcji jakości do przeprowadzenia optymalizacji systemu musimy dobrać także parametry wejściowe – zmienne decyzyjne. Dla przeprowadzonej optymalizacji dobrano 6 różnych parametrów decyzyjnych. Jak wspomniano, optymalizacja systemu była przeprowadzona w oparciu o algorytm genetyczny przy użyciu programu MOO (EPFL) współpracującego z modelem OSMOSE. Populacja początkowa liczyła 100 losowo dobranych osobników, które były ulepszane w 500 iteracjach algorytmu.
Wyniki optymalizacji wielokryterialnej zostały pokazane na diagramie Pareto na rys. 3. Możemy zauważyć, że dla kosztów inwestycyjnych najlepsze rezultaty to te z najmniejszą wartością (naszym celem jest minimalizacja nakładów). Z drugiej strony sprawność egzergetyczna powinna być maksymalnie zwiększana (system pracuje wtedy w najbardziej efektywny sposób). Na grafie łatwo zaobserwować, iż te dwa wskaźniki konkurują ze sobą. Aby lepiej zilustrować te różnice, warto przeanalizować wykresy linii Composite Curves z analizy Pinch Point systemu dla punktów z poszczególnych grup oznaczonych na rys. 3.
Na rys. 4 zaprezentowano system, przy tworzeniu którego najważniejsze były koszty początkowe inwestycji (punkt z grupy 1). Sprawność osiągana w nim to 40 % (w porównaniu do 62 % w najlepszym przypadku), z drugiej strony koszty inwestycyjne wynoszą 4,11 mln $ (w porównaniu do 6,13 mln $ dla najdroższego przypadku). Ilość produkowanej energii w tym układzie jest stosunkowo niewielka – jest to spowodowane przez niskie temperatury czynnika. Ponadto na rys. 4 można zobaczyć, że ciepło potrzebne w mleczarni jest dostarczane bezpośrednio ze źródła geotermalnego. Z tego powodu podane koszty inwestycyjne mogą być niższe niż rzeczywiste – obliczenia nie uwzględniają potrzeby wybudowania niezbędnej infrastruktury do zapewnienia ciepła dla mleczarni.
Punkt drugi można traktować jako złoty środek między punktem z grupy 1 oraz 3. Linia Integrated Composite Curve dla tego systemu jest przedstawiona na rys. 5. Koszty początkowe są co prawda wyższe niż w poprzednim przypadku (5,25 mln $), jednak układ osiąga wyższą sprawność – 51 %.
Na rys. 6 zaprezentowano system osiągający wysoką sprawność. Jak widać zostały osiągnięte 3 punkty Pinch Point. Czwarty punkt Pinch Point także jest prawie osiągnięty. System mógłby dawać jeszcze lepsze rezultaty, gdyby optymalizacja była przeprowadzona w większej liczbie iteracji algorytmu. Także wybranie większej populacji początkowej mogłoby poprawić rezultaty.
Optymalizacja modelu daje dobre rezultaty, jednak jest bardzo czasochłonna. Uzyskanie przedstawionych wyników zajmuje kilka godzin, ze względu na długotrwałe obliczenia dla każdego z pojedynczych modeli (wymagają rozwiązania dużych układów równań, a także integracji kilku różnych programów: VALI, OSMOSE, MOO). Zastosowanie techniki modelowania zastępczego pozwala na eliminację tego problemu. Obliczenia dla modelu tradycyjnego (dla pojedynczego przypadku) trwały około pół minuty. Dla modelu zastępczego czas obliczeń był niezauważalny. Poniżej zaprezentowano wyniki modelowania zastępczego dla jednej z funkcji dopasowania – kosztów inwestycyjnych systemu.
|
Liczba próbek |
Błąd średniokwadratowy |
Współczynnik korelacji R |
|
| Zbiór uczący | 753 | 2,18·10–3 | 99,33 % |
| Zbiór walidujący | 161 | 3,00·10–3 | 98,13 % |
| Zbiór testujący | 161 | 3,56·10–3 | 98,75 % |
Modele zastępcze zbudowano na podstawie Sztucznej Sieci Neuronowej zamodelowanej w środowisku MATLAB. Budowę każdej z sieci przedstawia rys. 7. Modele zastępcze stworzone w tym rozdziale bazują na 1075 punktach wygenerowanych losowo. Zbiór ten został podzielony na trzy części: zbiór uczący (70 %), zbiór walidujący (15 %) oraz zbiór testujący (15 %).
Rezultaty uzyskane w wyniku modelowania zastępczego pokazuje rys. 8. Pozioma oś obrazuje rzeczywiste odpowiedzi modelu dla konkretnych parametrów wejściowych, natomiast na osi pionowej pokazano wyniki zwracane przez model zastępczy. Dopasowanie (i działanie modelu zastępczego) byłoby idealne, gdyby wszystkie punkty leżały na przekątnej wykresu. Odchylenia od tej linii reprezentują błędy działania modelu zastępczego.
Pierwsza próba modelowania zastępczego nie dała oczekiwanych rezultatów. Dopiero po normalizacji wartości kosztów inwestycyjnych, przeskalowaniu do przedziału [-1, 1], uzyskano dobrze działającą sieć neuronową.
Dokładne rezultaty działania sieci neuronowej przedstawiono w tablicy. Model zastępczy daje dobre rezultaty: wartości współczynnika R dla wszystkich zbiorów są większe od 98 %.
Przedstawiony przykład pokazuje dwa sposoby wykorzystania sztucznej inteligencji w praktycznym problemie. Dzięki ich zastosowaniu dostaje się w prosty sposób rezultaty niemożliwe bądź trudne do wygenerowania tradycyjnymi metodami. Co więcej, daje on możliwość dalszego rozwijania tej tematyki – stworzenia systemu hybrydowego łączącego model zastępczy z algorytmem optymalizacyjnym.
Sztuczna inteligencja oferuje wiele rozwiązań, które czekają na przeniesienie do problemów praktycznych. W ciągle rozwijającej się dziedzinie nauki, jaką jest energetyka, wykorzystywanie tego typu metodologii wydaje się być bardzo dobrą drogą ku większej efektywności i wydajności.
Bibliografia
- Beccali, M., Cellura, M., Lo Brano, V., Marvuglia, A.: Forecasting daily urban electric load profiles using artificial neural networks. “Energy Conversion and Management” 45/2004, s. 2879–2900.
- Goldberg, D.: Algorytmy genetyczne i ich zastosowania. WNT, Warszawa 1995.
- Hahn, H., Meyer-Nieberg, S., Pickl, S.: Electric load forecasting methods: Tools for decision making. “European Journal of Operational Research” Volume 199, Issue 3, 2009.
- Jun, Z., Junfeng, L., Ngan H.W.: A multi-agent solution to energy management in hybrid renewable energy generation system. “Renewable Energy” 36/2010, s. 1352–1363.
- Kahraman, C., Kaya, I., Cebi, S.: A comparative analysis for multiattribute selection among renewable energy alternatives using fuzzy axiomatic design and fuzzy analytic hierarchy process.” Energy” 34/2009, s. 1603–1616.
- Kalogirou, S.: Artificial neural networks in renewable energy systems applications: a review. “Renewable and Sustainable Energy Reviews” 5/2001, s. 373–401.
- Khadir, M., Fay, D., Boughrira, A.: Day Type Identification for Algerian Electricity Load using Kohonen Maps. “International Journal of Mathematical and Computer Sciences” 1:2 2005.
- Ściążko, A., Kurcz, L.: Modelowanie i optymalizacja złożonego systemu energetycznego. „Zeszyty STN” 22/2011.
- Świrski, K., Wojdan K.: Immune Inspired Optimizer of Combustion Process in Power Boiler. Proceedings of 20th International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems, IEA/AIE 2007, New Trend in Applied Artificial Intelligence, Springer Verlag, Kyoto 2007, Japan.
- Sreekanth, J., Datta, B.: Multi-objective management of saltwater intrusion in coastal aquifers using genetic programming and modular neural network based surrogate models. “Journal of Hydrology” 393/2010, 245–256.
- Tadeusiewicz, R.: Sieci neuronowe. Akademicka Oficyna Wydawnicza RM, Warszawa 1993.
mgr inż. Anna Ściążko
Ukończyła w roku 2011 studia magisterskie w dziedzinie energetyki odnawialnej w RES (The School for Renewable Energy Science, Islandia). Pracę magisterską dotyczącą Modelowania Zastępczego Złożonych Systemów Elektroenergetycznych przygotowała w EPFL (Politechnika w Lozannie, Szwajcaria). W tym samym roku obroniła także pracę inżynierską na AGH (Wydział Energetyki). Praca inżynierska została przygotowana pod opieką dr. inż. Leszka Kurcza. Autorka obecnie kończy studia magisterskie w dziedzinie Energetyki (AGH) oraz Informatyki (UJ).




![Rys. 1. Schemat systemu [Schema of the system] Rys. 1. Schemat systemu [Schema of the system]](/var/aol/storage/images/artykuly/sterowanie/zastosowanie-metod-sztucznej-inteligencji-w-energetyce/62418-2-pol-PL/Zastosowanie-metod-sztucznej-inteligencji-w-energetyce_articleimage.jpg)
![Rys. 1. Schemat systemu [Schema of the system] Rys. 1. Schemat systemu [Schema of the system]](/var/aol/storage/images/media/par/07_11/sciazko/rysunek1.jpg/78724-1-pol-PL/rysunek1.jpg_large.jpg)
![Rys. 2. Elektrociepłownia – cykl ORC [CHP power plant - ORC cyckle] Rys. 2. Elektrociepłownia – cykl ORC [CHP power plant - ORC cyckle]](/var/aol/storage/images/media/par/07_11/sciazko/rysunek2.jpg/78727-1-pol-PL/rysunek2.jpg_medium.jpg)
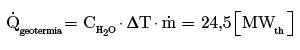
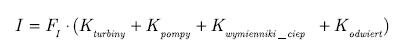
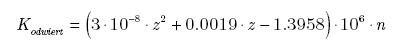

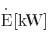
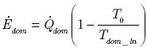
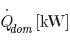
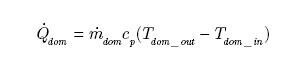
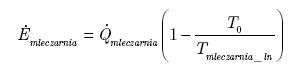
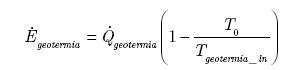
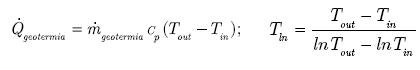
![Rys. 3. Linia Pareto dla optymalizacji Sprawność egzergetyczna – koszty [Inwestycyjne/Pareto· diagram for optimization Exergy efficiency – Investment cost] Rys. 3. Linia Pareto dla optymalizacji Sprawność egzergetyczna – koszty [Inwestycyjne/Pareto· diagram for optimization Exergy efficiency – Investment cost]](/var/aol/storage/images/media/par/07_11/sciazko/rys3.jpg/78763-1-pol-PL/rys3.jpg_medium.jpg)
![Rys. 4. Punkt z Grupy 1 [Point from Group 1] Rys. 4. Punkt z Grupy 1 [Point from Group 1]](/var/aol/storage/images/media/par/07_11/sciazko/rysunek4.jpg/78766-1-pol-PL/rysunek4.jpg_medium.jpg)
![Rys. 5. Punkt z Grupy 2 [Point from Group 2] Rys. 5. Punkt z Grupy 2 [Point from Group 2]](/var/aol/storage/images/media/par/07_11/sciazko/rysunek5.jpg/78769-1-pol-PL/rysunek5.jpg_medium.jpg)
![Rys. 6. Punkt z Grupy 3 [Point from Group 3] Rys. 6. Punkt z Grupy 3 [Point from Group 3]](/var/aol/storage/images/media/par/07_11/sciazko/rysunek6.jpg/78772-1-pol-PL/rysunek6.jpg_medium.jpg)
![Rys. 7. Schemat Sieci Neuronowe [Neural Network schema] Rys. 7. Schemat Sieci Neuronowe [Neural Network schema]](/var/aol/storage/images/media/par/07_11/sciazko/rysunek7.jpg/78775-1-pol-PL/rysunek7.jpg_medium.jpg)
![Rys. 8. Model zastępczy dla kosztów inwestycyjnych [Surrogate model for investment cost] Rys. 8. Model zastępczy dla kosztów inwestycyjnych [Surrogate model for investment cost]](/var/aol/storage/images/media/par/07_11/sciazko/rysunek8.jpg/78778-1-pol-PL/rysunek8.jpg_large.jpg)