Sterowanie amortyzacją dobiegu siłownika elektropneumatycznego
Paweł Langwald, Mariusz Jurczyński, Mariusz Olszewski print
![Rys. 1. Schemat budowy układu pneumatycznego stanowiska badawczego sterowanej amortyzacji [Schematic diagram of the electro-pneumatic research stand for the end position cushioning control] Rys. 1. Schemat budowy układu pneumatycznego stanowiska badawczego sterowanej amortyzacji [Schematic diagram of the electro-pneumatic research stand for the end position cushioning control]](/var/aol/storage/images/artykuly/inne/sterowanie-amortyzacja-dobiegu-silownika-elektropneumatycznego/60676-2-pol-PL/Sterowanie-amortyzacja-dobiegu-silownika-elektropneumatycznego_articleimage.jpg)
Rys. 1. Schemat budowy układu pneumatycznego stanowiska badawczego sterowanej amortyzacji [Schematic diagram of the electro-pneumatic research stand for the end position cushioning control]
W pracy przedstawiono koncepcję amortyzacji dobiegu siłownika pneumatycznego zrealizowaną na drodze niezależnego napełniania i opróżniania komory czynnej i biernej. Przedstawiono również rozwiązanie problemu modelowania siłownika pneumatycznego opartego na stworzeniu środowiska do symulacji procesów ruchu tłoka przy różnych koncepcjach sterowania.
Na przestrzeni ostatnich lat liczba elementów wykonawczych stosowanych na liniach montażowych produkcji przemysłowej stale rosła. Wobec automatyzacji i robotyzacji kolejnych gałęzi przemysłu należy spodziewać się, że tendencja ta zostanie zachowana. Wśród wykorzystywanych układów napędowych istotną rolę odgrywają napędy elektropneumatyczne. Okazują się one niezastąpione w prostych, ale bardzo licznych przypadkach przemieszczania (Pick and Place).
Podczas pracy tłok siłownika poddawany jest ciągłym zmianom prędkości: przyspieszaniu w początkowej fazie ruchu oraz gwałtownemu hamowaniu, najczęściej przez uderzenie w amortyzator lub ogranicznik ruchu, w końcowej fazie ruchu. Proces ten z nieznacznie zmienionymi parametrami ruchu odbywa się również w przeciwnym kierunku (powrót tłoka). W niewielu tylko aplikacjach stosowana jest ciągła kontrola położenia i/lub prędkości ruchu tłoka siłownika (sterowanie pozycyjne [1]). Powodem tego są koszty związane z koniecznością stosowania proporcjonalnych rozdzielaczy przepływowych i współpracujących z nimi przetworników pomiarowych w całym zakresie ruchu.
W celu wyeliminowania niekorzystnych w eksploatacji, gwałtownych zmian przyspieszenia związanych z hamowaniem elementów przez uderzenie oraz aby usunąć niepożądane finansowo skutki stosowania rozwiązań serwonapędowych w Instytucie Automatyki i Robotyki, podjęto prace badawcze nad sterowaną amortyzacją dobiegu tłoka siłownika, z wykorzystaniem konwencjonalnych rozdzielaczy.
Opis stanowiska badawczego
W skład laboratoryjnego stanowiska badawczego wchodzą (rys. 1):
- siłownik standardowy (znormalizowany), z jednostronnym tłoczyskiem, o zakresie ruchu 500 mm
- zawór redukcyjny z upustem (P)
- analogowy przetwornik ciśnienia (P1, P2, P3, P4)
- analogowy przetwornik przepływu (F1)
- standardowy zawór rozdzielający (5/2 – bistabilny) oraz zawory szybkiego działania (3/2 – monostabilne)
- analogowy przetwornik położenia działający w całym zakresie ruchu tłoka oraz analogowe przetworniki położenia o zakresie 50 mm, umieszczone na końcach siłownika.
Akwizycję danych oraz generowanie sygnałów sterujących zapewnia karta kontrolno-pomiarowa współpracująca ze środowiskiem MATLAB.
Model procesu ruchu tłoka siłownika pneumatycznego
W bardzo dużym uproszczeniu proces ruchu tłoka siłownika obciążonego masą m opisuje równanie równowagi sił [1, 3]:
| (1) | |
| (2) |
gdzie: m – masa części ruchomych, x – przemieszczenie tłoka z obciążeniem masowym m, F − łączna siła tarcia uszczelnienień tłoka i tłoczyska oraz prowadnic obciążenia masowego, P – zewnętrzne obciążenie siłowe, PC – wypadkowa siła działania ciśnień w komorach siłownika na tłok, pa − ciśnienie atmosferyczne, p1, p2− ciśnienia bezwzględne w komorach siłownika, A1, A2− powierzchnie czynne tłoka, R − reakcja pokrywy siłownika na tłok (w lewym skrajnym położeniu tłoka).
Reakcja pokrywy jest siłą bierną, która pojawia się, gdy tłok wywiera na nią nacisk. Przyjmując, że siły o zwrocie w prawo (rys. 1) są dodatnie, można zapisać, że:
- dla x = 0 i PC + P ≤ 0 → R = –(PC – P)
- dla x = 0 i PC + P > 0 → R = 0
- dla x> 0 → R = 0.
Rozwiązania równania (1) zależą od przebiegu sił tarcia F, sił oddziaływań zewnętrznych P i ciśnień w komorach siłownika.
W pozycji początkowej tłoka (przemieszczenie x = 0), siłę tarcia F reprezentuje tylko tarcie statyczne. Przyjęto, że:
- dla x = 0 i PC + P F = 0
- dla x = 0 i PC + P ≥ 0 → F = –min(F1, PC + P),
gdzie: F1 − maksymalna wartość siły tarcia statycznego.
W fazie hamowania, w chwili, w której po raz pierwszy zaczyna zmniejszać się wartość prędkości, wartość siły tarcia opisuje równanie:
| (3) |
gdzie: F2 – minimalna wartość siły tarcia dynamicznego, kv – współczynnik tarcia dynamicznego, v – prędkość ruchu tłoka, v0 – współczynnik określający szybkość zmian funkcji wykładniczej [2].
W dalszej fazie ruchu tłoka siłę tarcia opisuje równanie:
| (4) |
Zmiany ciśnienia powietrza w komorze napełnianej i opróżnianej siłownika opisują wyrażenia:
| (5) | |
| (6) |
gdzie: n – wykładnik przemian gazowych, x01, x02 – położenia martwe tłoka, R – stała gazowa dla powietrza, T0, p0 – temperatura i ciśnienie powietrza zasilającego, G1, G2 – masowe natężenie powietrza wpływającego i wypływającego z komór siłownika.
Do wyznaczania wartości G1 i G2 wykorzystano dla przepływów podkrytycznych zależności:
| (7) | |
| (8) |
i zależności odpowiednio uproszczone w przypadku przepływów krytycznych, gdzie: C1, C2 – przewodności dźwiękowe oporu pneumatycznego wlotowego i wylotowego, ρN, TN – gęstość i temperatura powietrza w znormalizowanej atmosferze odniesienia, T2 – temperatura w komorze opróżnianej (wyznaczana z założonej przemiany gazowej), ε1, ε2 – stosunki ciśnień za oporami do ciśnień przed oporami, b – rzeczywisty krytyczny stosunek ciśnień (przyjęto jednakowy dla obu oporów).
Wykorzystując opracowany na podstawie powyższych zależności model analityczny, można wyznaczyć, dla założonych wartości poszczególnych parametrów, przebiegi przemieszczenia, prędkości, przyspieszeń oraz ciśnień w procesach pozycyjnego przestawiania tłoka siłownika. Na podstawie powyższego algorytmu został opracowany program umożliwiający symulacyjne badanie dynamiki napędu siłownikowego w trakcie hamowania oraz badanie opracowywanego algorytmu sterowanej amortyzacji dobiegu.
Wyniki symulacji i badań eksperymentalnych
Proces hamowania powinien odbywać się na najkrótszej drodze ruchu tłoka w możliwie najkrótszym czasie, z siłą hamującą nieprzekraczającą granicznej, technologicznie określonej wartości. Wobec powyższych założeń, właściwe hamowanie powinno być realizowane ruchem jednostajnie opóźnionym.
W badanym algorytmie sterowanej amortyzacji założono hamowanie tłoka przy sterowanych zmianach ciśnienia komory napełnianej i opróżnianej siłownika (rys. 3).
Sterowanie zaworami monostabilnymi 3/2, swobodnie opróżniającymi komorę bierną i napełniającymi komorę czynną siłownika pozwala na uzyskanie sterowanego hamowania z wykorzystaniem przeciwciśnienia. W układzie tym możliwe jest uzyskanie łagodnego charakteru fazy hamowania dzięki rozdzieleniu sygnałów sterujących ciśnieniem w komorach siłownika (rys. 4 i 5).
W przeprowadzonej symulacji nie uwzględniono długości przewodów zasilających oraz zmiany natężenia przepływu w trakcie przełączania zaworu. Dodatkowo wprowadzono uproszczenia podczas wyznaczania siły tarcia.
Podsumowanie
Rzeczywiste przebiegi hamowania siłowników odpowiadają charakterystykom symulacyjnym w stopniu minimalnie satysfakcjonującym. Powodem największych trudności, pomijając uogólnienia poczynione w realizacji modelu, jest odtwarzanie prędkości z silnie zaszumionego sygnału położenia. Parametry hamowania, uzyskane na drodze symulacji, nie gwarantują dostatecznie dobrych wyników hamowania w czynnym eksperymencie. Dodatkowo wymagają one korekty, każdorazowo przy zmianie masy elementów przemieszczanych (rys. 6).
W Instytucie Automatyki i Robotyki trwają obecnie prace nad próbą szacowania wartości przemieszczanej masy zewnętrznej w oparciu o dane z przetwornika położenia (oraz prędkości jako wartości odtworzonej) w początkowej (50 mm) fazie ruchu tłoka siłownika. Uzyskane na tej drodze informacje posłużą do automatycznego doboru nastaw (przedziałów wysterowania zaworów) procesu hamowania.
Bibliografia
- Olszewski M.: Sterowanie pozycyjne pneumatycznego napędu siłownikowego, Oficyna Wydawnicza Politechniki Warszawskiej, Warszawa 2002.
- Kościelny W.J., Jurczyński M.: Pnematyczne adsorbery energii. Pneumatyka 5/2006, 24-26.
- Olszewski M.: Basics of Servopneumatics. VDI Verlag, Düsseldorf 2007.
mgr inż. Paweł Langwald
Absolwent Wydziału Mechatroniki Politechniki Warszawskiej. Doktorant w Zakładzie Urządzeń Wykonawczych Automatyki i Robotyki Instytutu Automatyki i Robotyki. W pracy naukowo-badawczej zajmuje się diagnostyką oraz algorytmami sterowania pneumatycznych urządzeń wykonawczych.
mgr inż. Mariusz Jurczyński
Absolwent Wydziału Mechatroniki Politechniki Warszawskiej. Asystent w Zakładzie Urządzeń Wykonawczych Automatyki i Robotyki Instytutu Automatyki i Robotyki.
prof. nzw. dr hab. inż. Mariusz Olszewski
Absolwent, obecnie profesor, od 1994 r. dyrektor Instytutu Automatyki i Robotyki na Wydziale Mechatroniki Politechniki Warszawskiej, stypendysta niemieckiej Fundacji Alexandra v. Humboldta, członek konsorcjum Europejskiej Sieci Centrów Techniki Płynowej (FPCE). Staże naukowe w Reńsko-Westfalskiej Politechnice w Akwizgranie i Uniwersytecie Technicznym w Stuttgarcie, praktyki w niemieckim przemyśle precyzyjnym i mechatronicznym. Specjalista i autor publikacji, książek, podręczników, patentów i wdrożeń z zakresu budowy i sterowania urządzeń wykonawczych automatyki, robotyki przemysłowej i mechatroniki. Wieloletnia praktyka w kierowaniu krajowymi i międzynarodowymi projektami badawczymi i rozwojowymi.




![Rys. 1. Schemat budowy układu pneumatycznego stanowiska badawczego sterowanej amortyzacji [Schematic diagram of the electro-pneumatic research stand for the end position cushioning control] Rys. 1. Schemat budowy układu pneumatycznego stanowiska badawczego sterowanej amortyzacji [Schematic diagram of the electro-pneumatic research stand for the end position cushioning control]](/var/aol/storage/images/media/par/11_10/langwald/1_dodac-ramke.jpg/77536-1-pol-PL/1_dodac-ramke.jpg_medium.jpg)
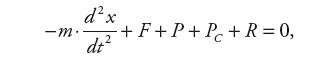
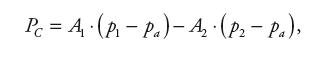
![Rys. 2. Schemat pneumatycznego, dławieniowego napędu siłownikowego [Schematic diagram of the electro-pneumatic system with the throttled drive] Rys. 2. Schemat pneumatycznego, dławieniowego napędu siłownikowego [Schematic diagram of the electro-pneumatic system with the throttled drive]](/var/aol/storage/images/media/par/11_10/langwald/2.jpg/77545-1-pol-PL/2.jpg_medium.jpg)
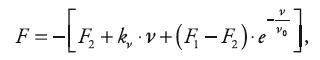
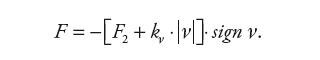
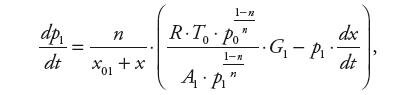
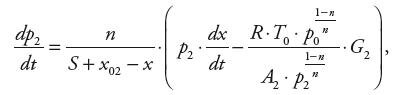
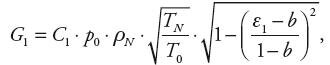
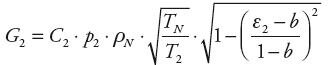
![Rys. 3. Uproszczony schemat hamowania przy sterowanych zmianach wartości ciśnienia w komorze napełnianej i opróżnianej [Oversimplify brake diagram with pressure control in the cylinder chambers] Rys. 3. Uproszczony schemat hamowania przy sterowanych zmianach wartości ciśnienia w komorze napełnianej i opróżnianej [Oversimplify brake diagram with pressure control in the cylinder chambers]](/var/aol/storage/images/media/par/11_10/langwald/3.jpg/77566-1-pol-PL/3.jpg_medium.jpg)
![Rys. 4. Charakterystyka zmian prędkości w funkcji czasu podczas hamowania z zaznaczonymi przedziałami wysterowania zaworu komory czynnej siłownika [Brake characteristic in the function of the time with time bracket of the valve control for active cylinder chamber] Rys. 4. Charakterystyka zmian prędkości w funkcji czasu podczas hamowania z zaznaczonymi przedziałami wysterowania zaworu komory czynnej siłownika [Brake characteristic in the function of the time with time bracket of the valve control for active cylinder chamber]](/var/aol/storage/images/media/par/11_10/langwald/4.jpg/77569-1-pol-PL/4.jpg_large.jpg)
![Rys. 5. Charakterystyka zmian prędkości w funkcji czasu podczas hamowania z zaznaczonymi przedziałami wysterowania zaworu komory biernej siłownika [Brake characteristic in the function of the time with time bracket of the valve control for passive cylinder chamber] Rys. 5. Charakterystyka zmian prędkości w funkcji czasu podczas hamowania z zaznaczonymi przedziałami wysterowania zaworu komory biernej siłownika [Brake characteristic in the function of the time with time bracket of the valve control for passive cylinder chamber]](/var/aol/storage/images/media/par/11_10/langwald/5.jpg/77572-1-pol-PL/5.jpg_large.jpg)
![Rys. 6. Charakterystyka zmian położenia i prędkości w funkcji czasu podczas rzeczywistego procesu hamowania z zaznaczonymi przedziałami wysterowania zaworu komory biernej siłownika [Position and velocity characteristic in the function of the time for real break process with time bracket of the valve control for passive cylinder chamber] Rys. 6. Charakterystyka zmian położenia i prędkości w funkcji czasu podczas rzeczywistego procesu hamowania z zaznaczonymi przedziałami wysterowania zaworu komory biernej siłownika [Position and velocity characteristic in the function of the time for real break process with time bracket of the valve control for passive cylinder chamber]](/var/aol/storage/images/media/par/11_10/langwald/6.jpg/77575-1-pol-PL/6.jpg_medium.jpg)