Dokładne pomiary wielkości geometrycznych za pomocą systemów wizyjnych
Marek Kania – Imaco (IMACO M. Kania Sp. K. ) drukuj
Systemy wizyjne realizują różnorodne zadania. W przypadku niektórych z nich, jak kontrola obecności, kontrola poprawności montażu, czytanie kodów lub tekstów, zliczenie elementów, często nie jest potrzebna zaawansowana analiza, by proces zakończył się sukcesem. Natomiast pomiarowe systemy wizyjne są obarczone wymaganiami o innej skali trudności.
Wielu integratorów systemów wizyjnych, zwłaszcza automatyków i informatyków, podejmuje się realizacji wizyjnych systemów pomiarowych, nie będąc świadomym metodyki ich projektowania i stopnia trudności. Poniżej przedstawiono wybrane zagadnienia dotyczące projektowania wizyjnego systemu pomiarowego. Nie wszystkie zadania wizyjne są bardzo skomplikowane. Realizacja wielu z nich może się udać z pominięciem przedstawionej poniżej analizy, zwłaszcza gdy zadanie pomiarowe jest proste, a wymagana dokładność pomiaru nie jest wysoka. Jeśli jednak błąd pomiaru ma być mały lub mierzonego wymiaru nie widać bezpośrednio na obrazie, pomiar jest pośredni, wówczas jest bardzo prawdopodobne, że bez dogłębnej analizy zadania i rachunku błędów projekt zakończy się niepowodzeniem.
1. Projektowanie urządzeń pomiarowych
Pomiar to porównanie mierzonego wymiaru z wzorcem. Oznacza to, że:
- albo przed pomiarem, np. po zmontowaniu systemu wizyjnego, system musi zostać skalibrowany na wzorcu i od momentu kalibracji do momentu pomiaru istotne parametry systemu (np. geometria układu) nie mogą ulec zmianie,
- albo w każdym pomiarze (w każdym obrazie) widoczny jest i mierzony obiekt, i wzorzec kalibracyjny.
Zarówno kalibracja początkowa, jak i jednoczesna rejestracja obrazu wzorca oraz obiektu wymagają zachowania pełnej kontroli nad geometrią systemu, zwłaszcza nad powiększeniem optycznym. Konsekwencją takiej definicji pomiaru jest definicja błędu pomiaru. Błąd pomiaru (E) jest sumą błędu kalibracji (Ek) i błędu porównania podczas pomiaru (Ep). Błąd systematyczny wyliczymy z sumy arytmetycznej:
| (1) |
a błędy przypadkowe lub zakres niepewności pomiarowej z sumy geometrycznej:
| (2) |
Sens praktyczny jest następujący:
- jeśli wzorzec ma stały błąd, np. „–0,2 mm”, a stały błąd porównania wynosił np. „+0,3 mm”, to błąd kalibracji wynosi: –0,2 +0,3 = +0,1 mm,
- jeśli przedział niepewności wymiaru wzorcowego wynosi np. „±0,2 mm”, a przedział niepewności dla samego pomiaru wzorca wynosi np. „±0,3 mm”, to błąd kalibracji wynosi: √ (0,2^2 + 0,3^2) = ±0,36 mm.
Model matematyczny
Pierwszym etapem projektowania układu pomiarowego jest stworzenie koncepcji i jej modelu matematycznego. Zmierzenie odległości dwóch krawędzi daje wynik „P” px. Najprostszy model matematyczny pomiaru odległości to:
| (3) |
gdzie: W – wymiar odległości krawędzi [mm], P – odległość zmierzona na obrazie [px], S – skala, czyli wynik kalibracji systemu [mm/px].
Przypadek nieco bardziej złożony to np. pomiar kąta pomiędzy dwiema krawędziami wykroju blachy (zakładam równą grubość wzorca i mierzonej blachy); rys. 1.
Po wyskalowaniu systemu na płaskim wzorcu uzyskamy skalę obrazu „S” [mm/px].
Wyznaczając z obrazu współrzędne X i Y czterech punktów (po dwa punkty na każdej krawędzi), uzyskujemy dane do obliczenia kąta pomiędzy tymi krawędziami.
| (4) |
Jak widać, wynik pomiaru kąta ALFA jest niezależny od skali „S”, a więc pomiar kąta nie wymaga kalibracji (jeśli pominiemy problem dystorsji obiektywu, czyli nierównomierności skali na obszarze obrazu).
Rachunek błędów = różniczka zupełna
Rachunek błędów oparty jest na różniczce zupełnej, która jest działaniem określającym, jak zmienia się wartość funkcji w wyniku zmian wartości zmiennych wejściowych.
| (5) |
Czyli: zmiana wartości funkcji równa jest sumie iloczynów zmian poszczególnych parametrów wejściowych i ich współczynników wpływów. Współczynnik wpływu danej zmiennej to pochodna cząstkowa funkcji po danej zmiennej.
Jeśli jako „zmiany parametrów wejściowych” wstawimy błędy poszczególnych wartości wejściowych, to jako wynik „dF” otrzymamy całkowity błąd pomiaru. W przypadku błędów systematycznych błędy elementarne sumuje się liniowo jak w równaniu (5). W przypadku błędów przypadkowych błędy elementarne sumuje się geometrycznie:
| (6) |
Rachunek błędów przypadkowych dla opisanego powyżej pomiaru kąta:
| (7) |
co po wyliczeniu różniczek:
| (8) |
oraz podstawieniu i przekształceniach da:
| (9) |
Nie wygląda zachęcająco, ale wyliczenie błędu to tylko kwestia pracy.
W pewnym zadaniu pomiaru kąta:
- o wielkości ok. 18°,
- kamerą o rozdzielczości 1280 × 960 pix i z polem widzenia ok. 40 × 30 mm (0,031 mm/px),
- przy zachowaniu dystansów w parze punktów pomiarowych 1–2 lub 3–4 równych ok. 400 px, przy rozdzielczości 0,031 mm/px, pomijając inne źródła błędów (np. dystorsję), uzyskaliśmy błąd pomiaru kąta ±0,29° tylko uwzględniając rozdzielczość 0,031 mm/px.
Jeśli taka wielkość błędu spełnia wymagania zadania pomiarowego – można budować system. Jeśli nie spełnia – trzeba weryfikować koncepcję i redukować błędy elementarne, np. poprawić rozdzielczość systemu, zmieniając kamerę lub zawężając pole widzenia.
2. Źródła błędów wizyjnego systemu pomiarowego
A. Światło (blooming, dyfrakcja, cienie)
Blooming to wada sensorów CCD, która nie występuje w sensorach CMOS. Objawia się powiększeniem powierzchni jasnych obszarów w przypadku prześwietlenia sensora kamery (rys. 2).
Aby wyeliminować błędy pomiarów wynikających z bloomingu, należy unikać prześwietlenia sensora, czyli ustawić poprawnie albo oświetlenie, albo czas ekspozycji, albo wzmocnienie kamery, albo przesłonę obiektywu, tak aby żaden piksel w obrazie nie był nasycony (równy 255 przy rozdzielczości 8 bit/px). Na rys. 2 efekt bloomingu jest wyraźny. W przypadku gdy nie jest on tak wyraźny, błąd pomiaru pojawi się, ale nie będziemy tego świadomi.
Dyfrakcja na krawędzi obiektu, przy oświetleniu tylnym (tła, czyli back light) to zjawisko normalne, występujące zawsze, ale jest to nieistotne przy pomiarach o małej dokładności.
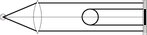
Typową koncepcję wizyjnego systemu pomiarowego do dokładnego pomiaru średnic wałków w skolimowanym świetle przechodzącym (back light) przedstawiono na rysunku 3.
Kolimator tworzy wiązkę równoległą, w której umieszczany jest mierzony obiekt. Profil rozkładu światła na sensorze nie jest prostokątem, tylko linią bardzo złożoną, a na granicy pomiędzy obszarami jasnymi i ciemnymi występują pochylone linie zmiany jasności (rys. 4).
Zależnie od doboru poziomu binaryzacji obrazu (np. w algorytmie wyszukiwania krawędzi) pomiar szerokości wałka wyjdzie różnie (rys. 5).
Optymalny poziom binaryzacji można dobrać podczas kalibracji na wałku o znanej średnicy. Trzeba wyszukać taki poziom, aby po binaryzacji algorytm pomiarowy wykazał średnicę zgodną z rzeczywistą średnicą wałka wzorcowego. Po takiej kalibracji, jak długo intensywność światła oświetlacza i geometria układu nie ulegną zmianie, tak długo kalibracja będzie ważna, a pomiar dokładny.
B. Optyka (skala, dystorsja, rozdzielczość)
Skala
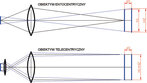
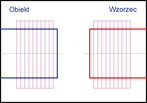
Do aplikacji pomiarowych najkorzystniejsze jest użycie obiektywu telecentrycznego, którego powiększenie jest stałe, niezależne od odległości obiektu od obiektywu (rys. 6). Jeśli nie można użyć obiektywu telecentrycznego, np. ze względu na zbyt duże wymiary obiektu, to konieczne jest użycie obiektywu entocentrycznego (standardowego). Aby utrzymać stałe powiększenie obiektywu entocentrycznego, konieczne jest utrzymanie stałego dystansu na linii obiekt – obiektyw. Można też zaniedbać stałość powiększenia i ciągle kontrolować dystans pomiędzy obiektem a obiektywem, np. za pomocą metody triangulacyjnej, a zmienność powiększenia wynikającą ze zmienności dystansu uwzględniać jako poprawkę w wynikach pomiarów.
Dystorsja
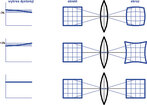
Dystorsja to deformacja obrazu wynikająca ze zmienności powiększenia obiektywu wraz ze zwiększaniem odległości od osi obiektywu (rys. 7).
Ponieważ producenci dobrych obiektywów udostępniają charakterystykę dystorsji i jest ona niezmienna dla serii obiektywów – można uwzględnić ją jako poprawkę błędu systematycznego.
Ze względu na nieliniową charakterystykę dystorsja jest szczególnie istotna przy pomiarach elementów zmieniających położenie w polu widzenia (rys. 8).
Przykładowo, przy polu widzenia 40 mm × 30 mm, z niedrogim obiektywem o dystorsji do 3 %, średnica wałka 14 mm
ulokowanego symetrycznie w polu widzenia, bez korekty na dystorsję, zmierzona będzie jako 14 – 1% – 1% = 14 – 2% = 13,72 mm, a średnica wałka ustawionego jedną krawędzią na środku pola widzenia, zaś drugą krawędzią w pobliżu brzegu pola widzenia, bez korekty na dystorsję, zmierzona będzie jako 14 – 0% – 3% = 14 – 3% = 13,58 mm.
Rozdzielczość obiektywu
Wpływa ona na ostrość krawędzi i na wykrywanie drobnych faktur. Niska rozdzielczość obiektywu zadziała podobnie jak dyfrakcja: rozmyje krawędzie i znów poprawność pomiaru zależna będzie od poprawności ustawienia poziomu binaryzacji obrazu.
C. Sensor kamery (rozdzielczość sensora, fill factor, równomierność rozstawu pikseli)
Rozdzielczość sensora jest głównym ograniczeniem możliwości systemu wizyjnego i jednym ze źródeł błędów, więc im mniejszy piksel i im wyższa rozdzielczość, tym mniejszy błąd pomiaru.
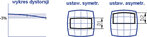
Fill factor to procentowy współczynnik wielkości powierzchni światłoczułej piksela w stosunku do całej powierzchni piksela (rys. 9). Większość kamer 2D używanych w widzeniu maszynowym ma sensory, w których fill factor wynosi 10–30 %, jeśli sensor nie ma mikrosoczewek, a dochodzi do 70 % w sensorach z mikrosoczewkami.
Przy małym fill factor pomiary bazujące na ocenie pozycji krawędzi mają pewne obszary nieczułości (rys. 10).
Zastosowanie rozdzielczości podpikslowej (interpolacja w obszarze 1 px) na poziomie 1:2–1:3 może mieć sens w przypadku kamer z sensorem IT CCD (Interline Transfer) lub CMOS, tylko jeśli sensory są wyposażone w mikrosoczewki. Jednak mikrosoczewki też nie są dużym ulepszeniem, bo ich zadaniem jest zwiększanie obszaru zbierania światła, bez względu na równomierność czułości optycznej piksela z mikrosoczewką. Wyższa rozdzielczość podpikslowa jest możliwa, jeśli sensor ma fill factor 100 %, czyli z kamerami liniowymi oraz z sensorami Frame Transfer i Full Frame. Niektóre z tych sensorów umożliwiają użycie rozdzielczości podpikselowej znacznie większej niż 1:10.
Równomierność podziału sensora na piksele to zagadnienie przemilczane przez cały rynek wizyjny. Jeśli w charakterystyce kamery podane jest, że piksel ma wymiar 7,4 µm, to wszyscy wierzą, że wszystkie piksele mają wymiar i rozstaw 7,400 ±0 µm, co nie jest prawdą. Żadna ze specyfikacji sensorów Sony lub Truesense nie podaje informacji o rozrzucie okresów pikseli. Obejściem problemu niepewności w zakresie nierównomiernego podziału sensora na piksele może być kalibracja, ale powinna ona być bardzo precyzyjna.
D. Szumy
Szumy kamery powodują nieznaczne lokalne zmiany jasności pikseli i mogą wpływać na lokalny wynik pomiaru, np. szukania krawędzi, o ile punkt pomiarowy trafi na piksel o zafałszowanej szumem wartości sygnału. Sposobem na redukcję wpływu szumów na wynik pomiaru jest albo uśrednianie wyniku z pomiarów na wielu pikselach, albo z pomiaru na wielu obrazach.
E. Algorytm (błędy i zaokrąglenia, uśrednianie i poprawki)
Algorytm to sposób obróbki danych pomiarowych. Jeśli algorytm nie zawiera błędów logicznych lub matematycznych, to dla optymalizacji pomiaru zalecane są:
- formatowanie liczb i wyników z wystarczająco dużą liczbą miejsc znaczących,
- wyliczanie i uwzględnianie poprawek na systematyczne błędy pomiaru, jak dystorsja, paralaksa, błąd skali, projekcja ukośna itp.,
- uśrednianie wyników obciążonych błędami przypadkowymi, będącymi poza naszą kontrolą, jak np. szumy, drgania obiektu, zmienne warunki otoczenia.
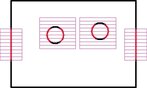
Uśrednianie może być realizowane jako liczba średnia z kilku liczb albo przez dopasowanie prostej lub krzywej do spróbkowanego konturu obiektu (np. metodą najmniejszych kwadratów) i wyliczenie parametrów tej prostej lub krzywej, np. wierzchołka łuku lub promienia łuku (rys. 11).
F. Kalibracja (wstępna lub jednoczesna)
Dokładność pomiarów systemu wizyjnego będzie gorsza niż dokładność kalibracji, czyli im lepsza kalibracja, tym większa szansa na dokładne pomiary. Kalibracja powinna obejmować całe pole widzenia i być zrobiona z dużą rozdzielczością (wzorzec w postaci gęstej kraty lub gęstej matrycy kropek). Najpopularniejsze wzorce kalibracji wstępnej to wydrukowane na drukarce laserowej matryce kropek lub krata. Na kartce A4 spodziewać się można dokładności wzorca rzędu 0,2–0,5 mm. Wzorce kropkowe szklane mają dokładność pozycji kropki rzędu ±1–2 µm.
Kalibrację jednoczesną uzyskamy, ustawiając taki wzorzec kropkowy jako tło mierzonego obiektu. Innym rozwiązaniem kalibracji jednoczesnej jest ustawienie w pobliżu mierzonego obiektu innego przedmiotu wzorcowego o znanej wielkości (rys. 12), a w analizie obrazu porównanie mierzonej wielkości z wielkością obiektu wzorcowego.
3. Pomiar 1. Pomiar wymiarów płaskiego wykroju blachy lub kartonu w oświetleniu tła (back light)
Ocena konturów w świetle przechodzącym to jedno z najłatwiejszych zadań pomiarowych. Jeśli mierzymy obiekty płaskie o stałej i bardzo małej grubości, możemy użyć obiektywu entocentrycznego, a po wyskalowaniu systemu na wzorcu kropkowym można mierzyć. W celu uzyskania możliwie wysokiej dokładności pomiarów długości i szerokości korzystnie jest wyznaczyć każdą krawędź konturu w wielu punktach (rys. 11) i do znalezionych punktów dopasować linie metodą najmniejszych kwadratów. Odległość naprzeciwległych linii daje poszukiwany wymiar konturu. Rozstawy otworów należy wyznaczyć jako odległość środków okręgów dopasowanych metodą najmniejszych kwadratów do punktów (rys. 11) znalezionych na krawędziach otworów.
Stosując metodę najmniejszych kwadratów do wyznaczenia linii konturów obiektu, można uzyskać błąd pomiaru mniejszy niż rozdzielczość pomiaru (niż wielkość piksela przeliczona na powierzchnię obiektu).
4. Pomiar 2. Dokładny pomiar średnicy wałka
Jeśli pomiar ma się odbywać na końcówce wałka, to jednoczesne wstawienie do pola widzenia końcówki wałka mierzonego i wałka wzorcowego (rys. 12) da możliwość dynamicznego dopasowania poziomu binaryzacji (thersholdu) do poprawnej oceny średnicy wałka mierzonego.
5. Pomiar 3. Pomiar kąta w dwóch wykonaniach
A. Podejście niemetrologiczne
Z obrazu jak na rys. 1 zdejmujemy współrzędne punktów charakterystycznych X1, Y1; X2, Y2; X3, Y3; X4, Y4.
Wyliczamy kąt z równania (2)
WYNIK = ALFA
B. Podejście metrologiczne
Z obrazu jak na rys. 1 zdejmujemy współrzędne punktów charakterystycznych X1, Y1; X2, Y2; X3, Y3; X4, Y4.
Wyliczamy kąt z równania (2)
Wyliczamy BŁĄD pomiaru z równania (9)
WYNIK = ALFA ± BŁĄD
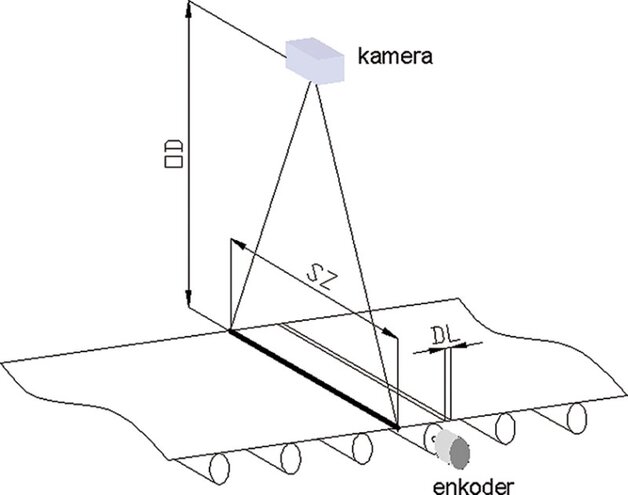
6. Pomiar 4. Skanowanie kamerą liniową
Kamera liniowa tworzy obraz z sumy kolejno rejestrowanych linii, których naświetlanie wyzwalane jest przez enkoder. Skala takiego skanera liniowego jest inna w kierunku ruchu skanera, a inna w kierunku poprzecznym. Kalibracja powinna wykazać dwie mniej lub bardziej różniące się skale wyrażone w mm/px.
W rzeczywistości skaner to dwa układy pomiarowe w jednym urządzeniu (rys. 13). Impulsy enkodera narzucają rozstaw linii obrazu, czyli skalę Y. Okres pikseli na sensorze, ogniskowa obiektywu i dystans roboczy narzucają skalę X. Zmiana enkodera lub rolek transportowych, a także zużycie rolek transportowych lub taśmy transportowej wymagają nowej kalibracji systemu w osi Y. Zmiana dystansu roboczego lub przeogniskowanie obiektywu wymaga nowej kalibracji w osi X.
O ile pomiary w osi X mogą być dosyć dokładne przy precyzyjnym prowadzeniu skanowanego obiektu, o tyle wysoka dokładność pomiaru w osi Y (w kierunku skanowania) wymaga dużej rozdzielczości enkodera, w miarę możliwości użycia enkodera programowalnego (w celu dopasowania rozdzielczości), małego bicia i małych błędów kołowości wałka napędowego, na osi którego zamocowany jest enkoder, oraz współosiowości enkodera z osią wałka napędowego. Dokładność rzędu ±0,01 mm w osi X jest realna, ale w osi Y trudna do uzyskania.
Zakończenie
Opisane wyżej aspekty należy rozważyć i przeliczyć przed zakupem komponentów do wizyjnego systemu pomiaru wielkości geometrycznych o dużej dokładności. W przypadku tworzenia systemu o bardzo wysokiej dokładności trzeba dodatkowo przeanalizować skutek uzmiennienia wszystkich stałych i zerowych wartości i źródeł błędów, zwykle pomijanych w analizie, np.:
- na rys. 3 – nieprostopadłość sensora do osi wiązki (sensor zarejestruje obraz rzutu ukośnego),
- odnośnie rys. 5 – winietowanie obiektywu daje nierówną jasność obrazu i właściwie poziom binaryzacji nie powinien być stały na całej powierzchni obrazu,
- typowy w analizie metrologicznej czynnik rozszerzalności termicznej (np. 1 °C zmiany temperatury pręta stalowego o długości 1 m daje zmianę długości 0,011–0,016 mm).
Dużo pracy, ale opłaci się. Dobrze przemyślany i przeliczony system będzie mierzył z oczekiwaną dokładnością i przez wiele lat. Największy problem w tym, żeby zleceniodawca był gotowy za tę pracę zapłacić.
Marek Kania
www.imaco.pl
źródło: IMACO




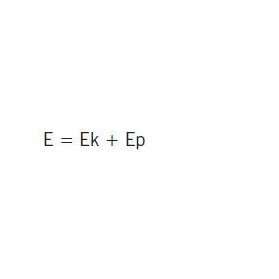
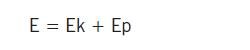
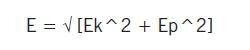


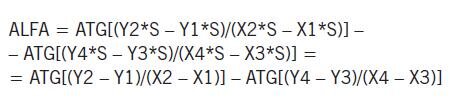
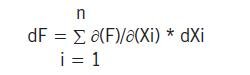
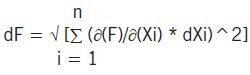
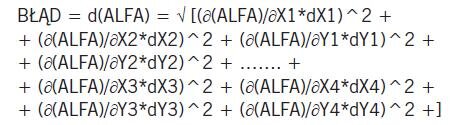

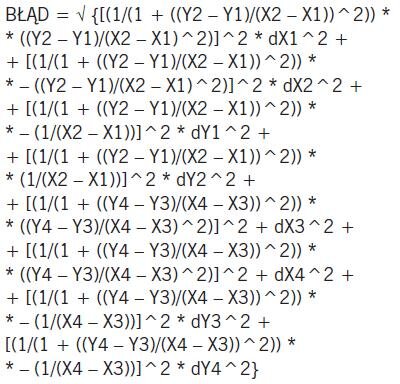





Komentarze
blog comments powered by Disqus