Zastosowanie identyfikacji opartej na wnioskowaniu rozmytym do identyfikacji modeli dynamicznych na przykładzie modelu protezy POLVAD
Krzysztof Janiszowski drukuj
Modelowanie dynamiki procesów staje się jednym z podstawowych sposobów badania układów w fazie tworzenia i badania prototypowych układów oraz ich sterowania. Technika ta (fast prototyping) jest podstawowym narzędziem dla projektowania nowoczesnych układów.
W pracy został przedstawiony sposób modelowania dynamicznych właściwości procesu z wykorzystaniem parametrycznych modeli rozmytych. Podejście to zostało zaprezentowane na przykładzie badania dynamiki sztucznej protezy serca POLVAD, przeprowadzonego na podstawie licznych eksperymentów testowych. We wstępie opisano badany proces i podkreślono pewne właściwości o charakterze nieciągłego działania, których występowanie ogólnie ogranicza zastosowanie opisu transmitancyjnego. Wyprowadzono podstawowe zależności do prowadzenia obliczeń parametrycznych modeli dynamicznych drogą oszacowań statystycznych dla modeli liniowych parametrycznych oraz modeli rozmytych. Przedstawiono wyniki badań optymalnego modelu liniowego i modelu rozmytego oraz przeprowadzono obszerną dyskusję uzyskanych modeli. Uzyskany opis dynamiki badanego procesu odtwarza wszystkie istotne zachowania badanego procesu w sposób całkowicie wystarczający do prowadzenia badań analizujących różne algorytmy sterowania lub regulacji, jak również umożliwia wprowadzenie np. optymalizacji pracy zaworów sterujących.
Modelowanie dynamiki procesów staje się jednym z podstawowych sposobów badania układów w fazie tworzenia i badania prototypowych układów oraz ich sterowania. Technika ta uzyskała już swoją nazwę – fast prototyping – i jest podstawowym narzędziem dla projektowania nowoczesnych układów oraz badania rozwiązań alternatywnych, poprzedzających wykonanie docelowych konstrukcji. Podstawą tego podejścia jest utworzenie zbioru modeli odtwarzających zachowanie komponentów układu. Modele takie można opracowywać na drodze analitycznych rozważań lub posługiwać się techniką identyfikacji. Jakkolwiek opis uzyskany drogą identyfikacji statystycznej wykazuje pewne ograniczenia, np. nie można z jego pomocą dokonywać optymalizacji działania zespołu, którego działanie zastępuje, ale ma również określone zalety, np. w przypadku istniejącego, gotowego zespołu może bardzo wiernie modelować jego zachowanie w układzie [2]. Przykład takiego zastosowania identyfikacji (opracowanie modelu dynamiki sztucznej protezy serca POLVAD) zostanie przedstawiony w artykule.
Modelowany proces – proteza POLVAD
Proteza POLVAD jest mechanicznym zespołem, który czasowo zastępuje pracę wybranej komory serca. Napęd tego urządzenia jest pneumatyczny, a zasada działania oparta na odtworzeniu cyklicznego, pulsacyjnego charakteru pompowania krwi do układu krążenia. Jej konstrukcję opracowano w Polsce i jest obecnie wykorzystywana w wielu szpitalach. Fotografia samej komory została pokazana na rys. 1.
Na rys. 2 są przedstawione oznaczenia podstawowych wielkości, umożliwiających właściwy opis tego zespołu oraz wielkości fizyczne mierzone podczas eksperymentów. Zespół POLVAD zasilany jest przepływem Fa powietrza o niskim poziomie ciśnienia Pzas, które mechanicznie przepycha elastyczną przeponę Sk i powoduje wyrzut krwi Fwyl przez otwartą zastawkę wylotową zwyl, gdy ciśnienie krwi Pk jest wyższe od ciśnienia krwi w kaniuli wylotowej Pwyl. W przypadku cyklu zasysania krwi ciśnienie Pwl powinno być większe od Pk, co spowoduje otwarcie zastawki wlotowej zwl i przepływ Fwl krwi do komory POLVAD. Oczywiście odpowiednie warunki zapewnia właściwe wysterowanie ciśnieniowe od strony zawory pneumatycznego Pa, który prowadzi do ciągłej wymiany strumienia powietrza Fa. Określony sposób sterowania czasowego powinien zapewniać całkowite opróżnienie komory z krwi (Vk=0 zapewnia brak zalegania krwinek i zapobiega zakrzepom) oraz odpowiednie opróżnienie komory powietrznej Va w zależności od zadanego poziomu wspomagania protezy POLVAD, a określonej przez zadaną objętość martwą komory powietrznej V . Opisany zespół zawiera bezwładnościowo działające zastawki mechaniczne, które zamykają lub otwierają określone kanały w sposób zbliżony do działania diod i tak były do tej pory modelowane [1, 5]. Zasada konstrukcji oraz działanie poszczególnych elementów wydają się proste i łatwe do zamodelowania mechanicznego, jednak obserwacje i przeprowadzone pomiary (Pwyl, Fwyl, Pzas, Fwl, Pwl) ujawniają zjawiska, które nie są zgodne z tak prostym podejściem do zachodzących zjawisk.
Na rys 3. przedstawiono przykładowo pomierzone (co 1 ms) zmiany ciśnień Pk, Pzas oraz przepływu Fwyl. Początek fazy wyrzutu jest zgodny z oczekiwaniami: Pzas przewyższa Pwyl (obie wielkości wyskalowane odrębnie!) i następuje wyrzut krwi Fwyl > 0 (dla lepszej rozróżnialności poziom 0 został zaznaczony dodatkową przerywaną linią).
Następnie poziom ciśnienia zasilającego maleje, przepływ wylotowy Fwyl zmniejsza się do dużej ujemnej wartości, a następnie wzrasta (zaznaczono te fazy przerywanymi strzałkami). Oznacza to, że zastawki nie działają jak diody oraz, że należy uwzględnić dodatkowe zjawiska przepływowe związane ze spójnością strugi, dynamiką zmian ciśnień, nieznaną zmienną bezwładnością strugi krwi itd.
W takim przypadku modelowanie zjawisk dynamicznych przestaje być prostym zadaniem, tym bardziej że badany zespół POLVAD mógł pracować w dość szerokim przedziale zmian: zadawanej średniej różnicy ciśnień, prędkości zmian (czasu cyklu) i procentowego czasu wypełnienia. W prowadzonych badaniach dobry model przepływu wylotowego był jednym z podstawowych czynników warunkujących prawidłowe zaprojektowanie całego układu sterowania, który powinien zapewniać odpowiednie warunki zasilania obwodu krążenia, przy jednoczesnej minimalizacji zużycia energii w celu zwiększenia czasu resursu urządzenia podczas zasilania autonomicznego. Poszukiwany model powinien uzależniać wielkość wyrzutu Fwyl od warunków zewnętrznych: ciśnienia wlotowego Pwl i przepływu wlotowego Fwl, ciśnienia wylotowego Pwyl oraz oczywiście sygnału sterującego Pzas (rys. 4).
Wielkości ΔP oraz τ oznaczają odpowiednio zadaną wartość różnicy ciśnień (średnie wylotowe względem średniego wlotowego) oraz czas wypełnienia cyklu – długość fazy wyrzutowej. Pozyskanie dobrego opisu, w formie podanej na rys. 4, zdecydowanie poprawiłoby jakość prowadzonych prac projektowych. Obok technik modelowych [1] zdecydowano się wykorzystać technikę identyfikacji rozmytej.
Rozmyty model dynamiki procesu
Załóżmy, że proces o przedstawionej wyżej strukturze można lokalnie przybliżyć za pomocą zestawu transmitancji operatorowych GFwyl Vj(s), zatem dla zerowych warunków początkowych sygnał wyjściowy z powyższego procesu byłby opisany zależnością:
| (1) |
gdzie transmitancje operatorowe GFwyl Vj(s) są określone przez odpowiednie współczynniki oraz wartości opóźnień:
| (2) |
i nieznane są wartości współczynników typu α oraz β jak również wartości opóźnień Tj. Wyznaczenie wartości tych współczynników wykonywane jest najczęściej w sposób pośredni metodą identyfikacji parametrycznej, tzn. w początkowym etapie wyznaczane są transmitancje dyskretne [2]:
| (3) |
na podstawie danych pomierzonych z określonym krokiem próbkowania Δ w taki sposób, aby modelowany sygnał wyjściowy był jak najbliższy pomierzonym wartościom Fwyl(kΔ), które uzależnione są od pomierzonych wartości sygnałów wejściowych Pwyl(kΔ), Pwl(kΔ), Fwl(kΔ), Pzas(kΔ) oraz nieznanych parametrów b0j, ..., aj:
| (4) |
gdzie tzw. wektor wejść do modelu v(kΔ) należący do zbioru RL zawiera sygnały pomierzone w odpowiednich (z uwzględnieniem opóźnień) chwilach czasowych (dla uproszczenia dalszych zapisów symbol Δ został pominięty)
| (5) |
a wektor kolumnowy θ należący do zbioru RL zawiera wartości nieznanych współczynników transmitancji (3)
| (6) |
Wektor współczynników θ może być oszacowany różnymi metodami. Jedną z najprostszych jest metoda najmniejszej sumy (LS) kwadratów błędów modelu (4), która pozwala dokonać oszacowania na podstawie znajomości kolumnowego wektora pomierzonych wyjść Y = [Fwyl(1),…, Fwyl(N)]T należący do zbioru RN, gdzie N oznacza liczbę pomiarów wielkości wyjściowej, oraz macierzy V należący do zbioru RNxL zawierającej N wierszowych wektorów wejść do modelu (4) w odpowiednich chwilach czasowych VT=[v(1)T, …, v(N)T]
| (7) |
Zaletą tej metody jest prosty, nierekursywny algorytm obliczeń. Następnie wartości współczynników wektora θLS są przekształcane drogą aproksymacji na współczynniki transmitancji GFwyl Vj(s) (2).
Model wyznaczony w taki sposób może bardzo dokładnie określać właściwości dynamiczne badanego procesu [3, 4], ale ma właściwości lokalne i w większości przypadków wymaga wyznaczenia wielu modeli, np. dla różnych warunków zasilania ΔP lub różnych czasów wypełnienia. Jednocześnie, w przypadku gdy występują zjawiska nieciągłe, np. działanie zaworu odcinającego, wówczas modele liniowe o opisie (2) lub (3) stają się niedokładne.
Bardzo korzystne w takim przypadku jest zastosowanie modeli rozmytych [1, 2, 6], tzn. modeli o takiej samej strukturze jak w (4), ale dla których wektor współczynników θ jest zmienny i uzależniony od tzw. zmiennej r rozmywającej (lub kilku zmiennych r1, r2, ...). Zmienna rozmywająca jest określona przez funkcje przynależności φi, (rys. 5). Na przykład, w przypadku, gdy zadana dla protezy POLVAD średnia różnica ciśnień ΔP między ciśnieniem na wylocie Pwyl oraz na wlocie Pwl będzie z obszaru pomiędzy 0 a 100 mmHg, wówczas obowiązywać będzie model θ1 (wektor współczynników) stosowny dla małej różnicy ciśnień - wyznaczony dla partycji θ1. Podobnie będzie w przypadku, gdy zmienna rozmywająca ΔP przyjmie wartość 145 mmHg, wówczas należy zastosować model θ2 wyznaczony dla średniej różnicy ciśnień ΔP, odpowiadający funkcji przynależności φ2.
Natomiast w przypadku zmiennej rozmywającej ΔP równej ~110 mmHg funkcja przynależności φ1 jest równa np. 0,7, a funkcja φ2jest równa 0,3 i wówczas model wynikowy jest kombinacją dwóch modeli θ = φ1θ1 + φ2θ2 = 0,7·θ1 + 0,3·θ2.
Ogólnie można wyznaczyć model rozmyty [2] w formie kombinacji liniowej modeli wyznaczonych dla różnych przedziałów funkcji przynależności. Przykładowo, dla dwóch zmiennych (w funkcji dyskretnej chwili czasu k) rozmywających r1(k) i r2(k), o odpowiednio p i q przedziałach funkcji przynależności postać modeli będzie następująca
| (8) |
Funkcje przynależności muszą spełniać określone warunki przy zastosowaniu powyższego formalizmu
| (9) |
dla dowolnej wartości zmiennej rozmywającej r(k). Model taki nazywany jest modelem TSK (Takagi-Sugeno-Kang).
Algorytm oszacowania wektorów modeli cząstkowych qi, przy wykorzystaniu modeli rozmytych, jest bardziej rozbudowany niż formuła (7) i wymaga jednoczesnego obliczenia wektorów dla wszystkich modeli θj, tzn. wyznaczenia wektora θT= [θT1, θT2, …, θTL] złożonego z L wektorów θi, który zapewni minimum wartości wskaźnika
| (10) |
Powyższe zagadnienie ma rozwiązanie w innej postaci [6]
| (11) |
i wymaga odwracania znacznie większych macierzy niż oszacowanie (7). Z tego powodu, przy tej formie modelu ważne jest tzw. uwarunkowanie numeryczne obliczeń, które określa poprawne wyznaczanie modeli cząstkowych. Wyznaczenie rodziny modeli cząstkowych (11) nie jest złożone obliczeniowo, a podstawową trudność stanowi właściwy dobór kształtu liczby funkcji przynależności. Istnieją również algorytmy [4, 7], które umożliwiają automatyczny dobór funkcji przynależności φi w taki sposób, by różnica między pomierzonym sygnałem y i jego oszacowaniem na podstawie modelu (11) była minimalna.
Podczas wyznaczania modelu rozmytego należy bardzo uważać na tzw. poziom walidacji poszczególnych modeli cząstkowych tzn. liczność zbioru danych, na podstawie którego został wyznaczony określony model lokalny θij
| (12) |
Wartość ta nie może być zbyt mała, tzn. kij >> μ (μ liczba współczynników w wektorze modelu θij), ponieważ w przeciwnym przypadku może zostać wyznaczony model θij o błędnie określonej dynamice, np. może być niestabilny. Zwykle przyjmuje się relację kij ≥ (10-20)μ za bezpieczne spełnienie warunku dobrego określenia modelu θij. Na poziom walidacji należy zwracać uwagę szczególnie przy większej liczbie sygnałów rozmywających, ponieważ w takim przypadku liczba modeli cząstkowych może być znaczna.
Modele parametryczne dynamiki protezy POLVAD
Parametryczny model dynamiki, odpowiadający schematowi oddziaływań z rys. 4, został oszacowany dla danych zarejestrowanych dla zadanej różnicy ciśnień ΔP = 100 mmHg. Parametry transmitancji (3) modelu (rząd n = 5, opóźnienia dj należący do zbioru [0, 30 ms]) zostały optymalnie dobrane w sensie minimum błędu odtwarzania sygnału przepływu wylotowego Fwyl. Jakość tego modelu jest przedstawiona na rys. 6, gdzie zamieszczono pomierzony i wyznaczony na podstawie modelu wycinek przebiegu wypływu Fwyl.
Na podstawie powyższych przebiegów można uznać, że wyznaczony model zachowuje się całkiem poprawnie, a wyznaczony średni poziom błędów ε, określony jako ∑|ε| / Σ|Fwyl|, był równy 23,5 %. Obserwowany efekt wstecznych przepływów, przedstawiony na rys. 3, który niepokoił zespół badający zjawisko, został odtworzony przez model w całkiem satysfakcjonujący sposób, zarówno pod względem amplitudy zmian, jak czasu trwania.
Należy jednak pamiętać, że przedstawione wyniki modelowania (rys. 6), były uzyskane dla tej samej sekwencji danych, na podstawie których był wyznaczany model, tzn. dla zadanego spadku ciśnienia ΔP = 100 mmHg. W przypadku wykorzystania tego modelu dla innej sekwencji, pomierzonej dla zadanej różnicy ciśnień ΔP = 135 mmHg (rys. 7), model ten był wyraźnie błędny i wykazywał średni poziom błędów 157 % (!), tzn. model odtwarzał zmiany, ale w mniejszym zakresie i na całkiem innym poziomie.
Taki efekt oznaczał, że można „wpasować” model do określonej sekwencji danych, ale będzie on miał charakter bardzo lokalny i trzeba znaleźć wiele takich modeli w celu właściwego odtwarzania sygnału Fwyl.
W celu właściwego odtworzenia właściwości dynamicznych postanowiono wykorzystać modele rozmyte. Jako zmienne parametryzujące wykorzystano dwa sygnały: sygnał przepływu Fwyl oraz sygnał zadanej różnicy ciśnień ΔP. W przypadku sygnału przepływu Fwyl postanowiono przeprowadzić rozmycie uzależniające właściwości modelu od stanu: przepływ dodatni (właściwy wyrzut), przepływ wsteczny (niedomknięta zastawka) oraz faza domykania zastawki, co spowodowało ustawienie funkcji przynależności jak na rys. 8.
W przypadku drugiej zmiennej rozmywającej model podział na funkcje przynależności wyglądał podobnie (również trzy obszary), przy czym za niską różnicę ciśnień przyjęto wartości bliskie ΔP < 125 mmHg, a za wysokie ΔP powyżej 160 mmHg (rys. 9).
Przy takiej parametryzacji podczas wyznaczania modelu rozmytego należało określić 9 modeli cząstkowych. Pomiary zostały przeprowadzone dla różnych zadanych wartości ΔP = 100, 135, 150, 165, 175 mmHg. W każdym cyklu było 10 tys. pomiarów, a wyznaczane modele cząstkowe były określone na podstawie od ok. 300 do ponad 6000 pomiarów (12). W celu oszacowania wykorzystano 3 cykle: ΔP = 100, 150, 175 mmHg, a w celu weryfikacji dodatkowo ΔP = 135, 165 mmHg. Porównawcze wycinki przebiegów zostały przedstawione na rys. 10. Można zaobserwować wyraźną zgodność przebiegów mierzonych i modelowanych. Błędy modelowania były dla sekwencji ΔP = 135 mmHg, największe i wynosiły 23,3 %, a dla sekwencji ΔP = 175 mmHg tylko 10,4 %. Należy przy tym zwrócić uwagę, że występujące błędy są w większości efektem niedoskonałości techniki pomiarowej.
Model dobrze odtwarzał przebiegi zarówno dla danych, na podstawie których był wyznaczany (ΔP = 100, 150, 175 mmHg) jak i dla danych weryfikacyjnych (ΔP = 135, 165 mmHg) i można go uznać za dobre odtworzenie zachowania badanego procesu – zachowania dynamicznego komory POLVAD.
W artykule nie będą dyskutowane poszczególne transmitancje modeli cząstkowych, bo jest ich dużo: 9 modeli, każdy zawiera 5 transmitancji rzędu 4. W celu zobrazowania zmienności wyznaczonych modeli zostały przedstawione (rys. 11), odpowiedzi skokowe modeli przepływu Fwyl na zmianę ciśnienia Pzas w zależności od obszarów, dla których był wyznaczany model cząstkowy, przy czym na wykresach podano wskaźnik funkcji przynależności dla obydwu zmiennych rozmywających oraz wielkość wzmocnienia statycznego K modelu cząstkowego. Przykładowo, Fwyl = 2 i ΔP = 3 oznacza model cząstkowy wyznaczony dla: Fwyl zawartego w przedziale [-0,5; 0,5] oraz ΔP > 165.
Komentując wyniki (rys. 10) można uznać, że wyznaczony model nie obniża poziomu reakcji na pobudzenia, co dość często występuje w modelach określanych za pomocą estymatora LS, gdy są obecne zakłócenia pomiarowe, jak w rozważanym przypadku. Może być zatem wykorzystany do modelowania protezy POLVAD w różnych warunkach pracy i sprawdzania różnych, możliwych do rozważenia sposobów pobudzania. Takim krytycznym parametrem aplikacyjnym urządzeń tego typu jest szybkość zmian przepływu podczas wyrzutu (zbyt duży gradient zmian przepływu powoduje rozbijanie czerwonych krwinek).
Z tego powodu stosowane algorytmy sterowania oraz reakcje serwozaworów, sterujących zmianą ciśnienia Pa w części pneumatycznej protezy, są bardzo istotnym problemem. Wyznaczony model bardzo zgodnie (z pomiarami) odtwarza ten fragment mierzonych przebiegów i należy uznać, że będzie się bardzo dobrze nadawał do prowadzenia dalszych prac badawczych.
Przedstawione wybrane odpowiedzi skokowe (rys. 11) również wykazują wyraźne różnice. Należy zwrócić uwagę na zmienny współczynnik wzmocnienia K, który w przypadku ostatniego modelu cząstkowego ma wartość ujemną. Świadczy to o zmienności dynamiki w zależności od sygnałów rozmywających, jak również o potrzebie poszukiwania różnych modeli cząstkowych.
Podsumowanie
Przedstawiony w artykule sposób wykorzystania metody wyznaczania modeli rozmytych do określania właściwości dynamicznych procesów, dla których nie jest znany dokładny model działania, jest bardzo efektywnym podejściem i może w znaczący sposób przyspieszać badania, upraszczać technikę modelowania i przyspieszać etap wstępnej analizy działania całości układu, który zawiera zespół lub proces zastąpiony modelem rozmytym. Jednocześnie fakt, że model wynikowy pozwala zastępować działanie procesu w szerokim zakresie zmian punktu pracy procesu, umożliwia prowadzenie obliczeń optymalizacyjnych i szybką analizę działania alternatywnych rozwiązań układu lub diagnozowania procesu.
Podziękowania
Powyższa praca była wynikiem badań sponsorowanych przez narodowy program badawczy „Polskie Sztuczne Serce”, zgodnie z umową nr 12/WK/P02/0001/SPB-PSS/2009.
Bibliografia
- Golnik A., Fajdek B., Janiszowski K.: Modelowanie układu krążenia z możliwością równoległego wspomagania pracy komór serca w pakiecie programowym PExSim. PAR 11/2010.
- Janiszowski K.: Identyfikacja parametryczna układów dynamicznych w przykładach. Exit, 2002.
- Janiszowski K. Wnuk P.: PexSim – a novel approach to the problem of the investigation of complex dynamic systems in an industrial environment. Problemy eksploatacji, 4/2006, s. 17–37.
- Janiszowski K.: Modele procesów. „Modelowanie diagnostyka i sterowanie nadrzędne procesami, Implementacja w systemie Diaster”, Pr. zb. Red. J. Korbicz, J.M. Kościelny, WNT 2009.
- Kozarski M., Ferrari G., Zielczyński K., Górczyńska K., Pałko K. J., Tokarz A., Darowski M.: A new hybrid electro-numerical model of the left ventricle. Computers in Biology and Medicine, vol.38, pp. 979–989, 2008.
- Wnuk P.: Algorytmy optymalizacji struktury rozmytych modeli. Rozprawa doktorska, Warszawa 2004.
prof. dr hab. inż. Krzysztof Janiszowski
Działalność naukowa w zakresie identyfikacji, modelowania i sterowania procesów. Autor 5 podręczników, 35 artykułów, 84 referatów i ponad 40 projektów badawczych. Obszary badań aplikacyjnych: identyfikacja procesów przemysłowych (pieca obrotowego w cementowni, pieca do ciągłego wytopu stali, reaktorów chemicznych, pieca pirolitycznego, walczaka parowego, zespołu oczyszczalni itd.), synteza algorytmów sterowania do pneumatycznych układów pozycjonujących, hydraulicznych napędów wyporowych, zespołu napędu hybrydowego o 2 stopniach swobody, oraz pakiety oprogramowania do identyfikacji układów dynamicznych (IDCAD), i modelowania, symulacji działania i sterowania procesów przemysłowych (PExSim).




![Rys. 1. Modelowana proteza komory serca POLVAD [Modelled hearth assisting device POLVAD] Rys. 1. Modelowana proteza komory serca POLVAD [Modelled hearth assisting device POLVAD]](/var/aol/storage/images/artykuly/sterowanie/zastosowanie-identyfikacji-opartej-na-wnioskowaniu-rozmytym-do-identyfikacji-modeli-dynamicznych-na-przykladzie-modelu-protezy-polvad/61066-2-pol-PL/Zastosowanie-identyfikacji-opartej-na-wnioskowaniu-rozmytym-do-identyfikacji-modeli-dynamicznych-na-przykladzie-modelu-protezy-POLVAD_articleimage.jpg)
![Rys. 1. Modelowana proteza komory serca POLVAD [Modelled hearth assisting device POLVAD] Rys. 1. Modelowana proteza komory serca POLVAD [Modelled hearth assisting device POLVAD]](/var/aol/storage/images/media/par/11_10/janiszowski/1.jpg/77965-1-pol-PL/1.jpg_large.jpg)
![Rys. 2. Schematyczne przedstawienie podstawowych wielkości w badanym zespole [Presentation of basic values in the modelled dynamic system] Rys. 2. Schematyczne przedstawienie podstawowych wielkości w badanym zespole [Presentation of basic values in the modelled dynamic system]](/var/aol/storage/images/media/par/11_10/janiszowski/2.jpg/77968-1-pol-PL/2.jpg_large.jpg)
![Rys. 3. Przykładowy wycinek pomiarów ciśnień: Pzas oraz Pwyl i przepływu Fwyl wykonany na stanowisku badawczym [Measured on laboratory stand exemplary transients of: pressures Pzas and Pwyl together with flow Fwyl] Rys. 3. Przykładowy wycinek pomiarów ciśnień: Pzas oraz Pwyl i przepływu Fwyl wykonany na stanowisku badawczym [Measured on laboratory stand exemplary transients of: pressures Pzas and Pwyl together with flow Fwyl]](/var/aol/storage/images/media/par/11_10/janiszowski/3.jpg/77971-1-pol-PL/3.jpg_medium.jpg)
![Rys. 4. Poszukiwany sposób opisu dynamiki komory POLVAD [Representation of investigated dynamics for the device POLVAD] Rys. 4. Poszukiwany sposób opisu dynamiki komory POLVAD [Representation of investigated dynamics for the device POLVAD]](/var/aol/storage/images/media/par/11_10/janiszowski/4.jpg/77974-1-pol-PL/4.jpg_medium.jpg)
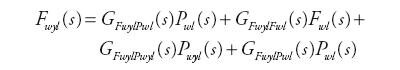
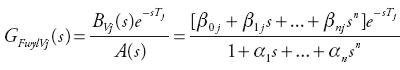
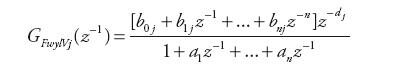
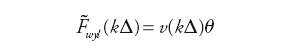
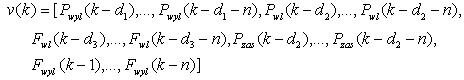
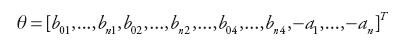
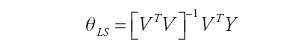
![Rys. 5. Przykładowe funkcje przynależności dla zmiennej rozmywającej będącej różnicą DP [Exemplary membership functions for fuzzy parameterization by the signal DP] Rys. 5. Przykładowe funkcje przynależności dla zmiennej rozmywającej będącej różnicą DP [Exemplary membership functions for fuzzy parameterization by the signal DP]](/var/aol/storage/images/media/par/11_10/janiszowski/5.jpg/77998-1-pol-PL/5.jpg_medium.jpg)
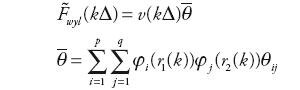
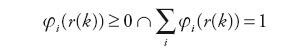
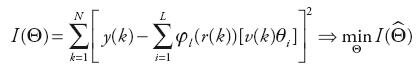
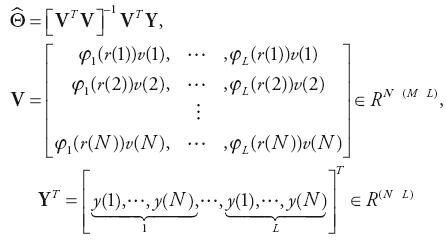
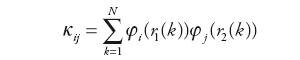
![Rys. 6. Modelowany i pomierzony wycinek przebiegu przepływu Fwyl dla modelu wyznaczonego na podstawie sekwencji ΔP=100 mmHg [Measured and modeled transients of flow Fwyl for the model estimated for a sequence ΔP=100 mmHg (appr. 800 ms)] Rys. 6. Modelowany i pomierzony wycinek przebiegu przepływu Fwyl dla modelu wyznaczonego na podstawie sekwencji ΔP=100 mmHg [Measured and modeled transients of flow Fwyl for the model estimated for a sequence ΔP=100 mmHg (appr. 800 ms)]](/var/aol/storage/images/media/par/11_10/janiszowski/6.jpg/78016-1-pol-PL/6.jpg_medium.jpg)
![Rys. 7. Modelowany i pomierzony wycinek przebiegu przepływu Fwyl (ΔP=135 mmHg) dla modelu wyznaczonego na podstawie sekwencji ΔP=100 mmHg [Measured transients of the flow Fwyl (ΔP=135 mmHg) and simulated by the model estimated for transients ΔP=100 mmHg] Rys. 7. Modelowany i pomierzony wycinek przebiegu przepływu Fwyl (ΔP=135 mmHg) dla modelu wyznaczonego na podstawie sekwencji ΔP=100 mmHg [Measured transients of the flow Fwyl (ΔP=135 mmHg) and simulated by the model estimated for transients ΔP=100 mmHg]](/var/aol/storage/images/media/par/11_10/janiszowski/7.jpg/78019-1-pol-PL/7.jpg_medium.jpg)
![Rys. 8. Określenie funkcji przynależności dla zmiennej rozmywającej Fwyl [Determination of membership functions for the parameter Fwyl] Rys. 8. Określenie funkcji przynależności dla zmiennej rozmywającej Fwyl [Determination of membership functions for the parameter Fwyl]](/var/aol/storage/images/media/par/11_10/janiszowski/8.jpg/78022-1-pol-PL/8.jpg_medium.jpg)
![Rys. 9. Funkcje przynależności dla zmiennej ΔP [Membership functions for the parameter ΔP] Rys. 9. Funkcje przynależności dla zmiennej ΔP [Membership functions for the parameter ΔP]](/var/aol/storage/images/media/par/11_10/janiszowski/9.jpg/78025-1-pol-PL/9.jpg_medium.jpg)
![Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber] Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber]](/var/aol/storage/images/media/par/11_10/janiszowski/10-1.jpg/78028-1-pol-PL/10-1.jpg_medium.jpg)
![Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber] Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber]](/var/aol/storage/images/media/par/11_10/janiszowski/10-2.jpg/78031-1-pol-PL/10-2.jpg_medium.jpg)
![Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber] Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber]](/var/aol/storage/images/media/par/11_10/janiszowski/10-3.jpg/78034-1-pol-PL/10-3.jpg_medium.jpg)
![Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber] Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber]](/var/aol/storage/images/media/par/11_10/janiszowski/10-4.jpg/78037-1-pol-PL/10-4.jpg_medium.jpg)
![Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber] Rys. 10. Zmierzone i modelowane wycinki przebiegów wartości wypływu z komory POLVAD za pomocą modelu rozmytego [Measured and modelled (by the fuzzy model) transients of the output flow from the POLVAD chamber]](/var/aol/storage/images/media/par/11_10/janiszowski/10-5.jpg/78040-1-pol-PL/10-5.jpg_medium.jpg)
![Rys. 11. Odpowiedzi skokowe przepływu Fwyl względem wysterowania Pa dla różnych modeli cząstkowych [Responses of flow Fwyl in respect of the step of control Pa for different partially models] Rys. 11. Odpowiedzi skokowe przepływu Fwyl względem wysterowania Pa dla różnych modeli cząstkowych [Responses of flow Fwyl in respect of the step of control Pa for different partially models]](/var/aol/storage/images/media/par/11_10/janiszowski/11.jpg/78043-1-pol-PL/11.jpg_large.jpg)
Komentarze
blog comments powered by Disqus