Sterowanie ślizgowe w zastosowaniu do serwonapędu elektrohydraulicznego
Arkadiusz Winnicki, Mariusz Olszewski print
![Rys. 1. Schemat budowy serwonapędu elektrohydraulicznego [Diagram of the structure of the electro-hydraulic servo system] Rys. 1. Schemat budowy serwonapędu elektrohydraulicznego [Diagram of the structure of the electro-hydraulic servo system]](/var/aol/storage/images/artykuly/inne/sterowanie-slizgowe-w-zastosowaniu-do-serwonapedu-elektrohydraulicznego/60702-2-pol-PL/Sterowanie-slizgowe-w-zastosowaniu-do-serwonapedu-elektrohydraulicznego_articleimage.jpg)
Rys. 1. Schemat budowy serwonapędu elektrohydraulicznego [Diagram of the structure of the electro-hydraulic servo system]
Przedstawimy model sterowania ślizgowego SMC (ang. Sliding Mode Control) w zastosowaniu do elektrohydraulicznego układu serwonapędu. Algorytm ślizgowy bardzo dobrze nadaje się do sterowania obiektami nieliniowymi oraz charakteryzuje się dużą odpornością na zakłócenia. Dużą niedogodnością sterowania ślizgowego są efekty częstych przełączeń sygnału sterowania (ang. Chattering Phenomena), co może prowadzić do powstawania drgań elementów wykonawczych i wpływać niekorzystnie na trwałość napędzanego urządzenia. W artykule zaprezentowano alternatywne podejście, które w znacznym stopniu eliminuje efekt częstych przełączeń.
Serwonapędy elektrohydrauliczne odgrywają ważną rolę w budowie maszyn produkcyjnych i roboczych współczesnego przemysłu. Zaletą napędów elektrohydraulicznych są bezkonkurencyjnie duże wydajności energetyczne i sztywności obciążeniowe aktuatorów. Implementacja układów sterowania napędów elektrohydraulicznych pozostaje jednak nadal nie w pełni zadowalająco rozwiązanym problemem. Jednym z głównych powodów są silne nieliniowości zachowań dynamicznych elementów i zespołów hydraulicznych [1]. Dla poprawy jakości tych zachowań wypróbowano w technice serwonapędu elektrohydraulicznego w zasadzie wszystkie znane algorytmy sterowania, zaczynając od konwencjonalnych regulatorów PID, przez regulatory zmiennych stanu, układy logiki rozmytej i kończąc na sieciach neuronowych. W ostatnich latach coraz większą popularność zdobywa nowe podejście do sterowania układami nieliniowymi w postaci sterowania ślizgowego [5, 7]. Sterowanie to należy do tzw. rozwiązań odpornych (ang. Robust Control) i doskonale nadaje się do obiektów o niedokładnie wyznaczonych parametrach modelu, a w odniesieniu do technik napędowych charakteryzuje się bardzo dobrymi wynikami pozycjonowania przestawnego i nadążania [2, 3, 6].
Model matematyczny
Model opisujący zachowania dynamiczne serwonapędu elektrohydraulicznego (rys. 1) można przedstawić jako układ równań trzeciego stopnia w przestrzeni zmiennych stanu [1]:
| (1) | |
| (2) | |
| (3) |
Pochodne ciśnień p1 i p2, wynikające z natężeń przepływu przez zawór rozdzielający, opisane są zależnościami:
| (4) | |
| (5) |
gdzie: B − moduł ściśliwości cieczy, VL1,2 − objętości martwe siłownika, xmax − skok tłoka, u − sygnał sterowania, pS,T − ciśnienia zasilania i spływu oraz Kq − stały współczynnik natężenia przepływu, który może być aproksymowany za pomocą danych katalogowych producenta zaworów rozdzielających.
Podstawiając równania (4) i (5) do (3), otrzymuje się następujące równanie stanu:
| (6) | |
| (7) | |
| (8) |
przy czym zmienne współczynniki β1 i β2 są funkcjami położenia tłoczyska x:
| (9) | |
| (10) |
Zachowanie dynamiczne układu, zależność (7), jest jedynie estymowane z określonym błędem oszacowania εf:
| (11) |
Błąd oszacowania εf zależy od zmiennych stanu obiektu: x, v oraz a. Przyjmując, że A1,2 i M są znane z dostateczną dokładnością, wartość błędu εf określa zależność
| (12) |
gdzie xr jest pozycją zadaną.
Nie jest możliwe dokładne ustalenie wartości współczynnika wzmocnienia sterowania b, zależność (8), a jedynie tylko oszacowanie jego wartości między wartościami bmin i bmax − dlatego wzmocnienie to możemy przyjąć jako średnią geometryczną tych wartości
| (13) |
którą, dzięki przekształceniu zależności (8), określi zależność:
| (14) |
gdzie g(x) jest równe
| (15) |
a pvmin, pvmax reprezentują minimalne i maksymalne spadki ciśnień przepływów przez kanały zaworu rozdzielającego.
Dla wektora błędu e = [ex, ev, ea] z elementami składowymi: ex = x–xr, ev = v–vr oraz ea = a–ar, definiuje się zmienną w czasie, skalarną powierzchnię przełączeń S(e, t) = 0, z S określonym jako [8]:
| (16) |
Sterowanie ekwiwalentne ueq, które dba aby trajektoria w przestrzeni stanu pozostawała na powierzchni przełączeń, jest określone z warunku na S´ = 0 i wyraża się zależnością
| (17) |
Wyznaczone sterowanie ekwiwalentne nie daje gwarancji stabilności sterowania ślizgowego. Aby skompensować błędy oszacowania (np. zmienność parametrów czy brak modelu tarcia), zależność (17) należy uzupełnić składnikiem nieciągłym w postaci funkcji signum (sign):
| (18) |
Analiza stabilności
Istotą algorytmu ślizgowego jest to, że aby osiągnąć idealne śledzenie, wszystkie trajektorie układu w przestrzeni stanu muszą dążyć do powierzchni S w skończonym czasie, a następnie pozostawać na tej powierzchni, co można wyrazić matematycznym warunkiem na zasadę zachowania stabilności (II metoda Lapunowa) [2, 7]:
| (19) |
gdzie η jest określoną, dodatnią stałą.
W równaniu (18) należy wyznaczyć zmienną k, tak aby powyższy warunek stabilności był spełniony. Wychodząc z pochodnej S, zależność (16),
| (20) |
przyjmując:
| (21) |
oraz korzystając z zależności (6, 18 i 20) można zapisać warunek (19) w następującej postaci:
| (22) |
Biorąc pod uwagę, że dla S = 0 warunek (19) jest oczywiście spełniony, z warunków (11) i (22), otrzymuje się
| (23) |
Korzystając z zależności (13) oraz wprowadzając stosunek wzmocnień:
| (24) |
dla 0 bmin ≤ b ≤ bmax, otrzymuje się
| (25) |
co, odwołując się do równania (17) i zapisu (21), określa końcowy warunek na wartość k jako:
| (26) |
Jeśli k spełnia warunek (26), to jednocześnie istnieje pewność, że warunek (19) na stabilność i ruch ślizgowy został spełniony.
Występowanie w zależności na sygnał sterowania członu nieciągłego w postaci funkcji signum (17, 18), powoduje pojawienie się częstych przełączeń [9]. Jednym z częstych rozwiązań eliminujących ten problem jest zastąpienie funkcji sign w zależności (18) przez funkcję tanh (sigmoidalną) [4]:
| (27) |
gdzie φ>0 jest użyty w celu wygładzania drgań sygnału sterowania. Wartość φ powinna zapewniać optymalny kompromis między błędem pozycjonowania a poziomem drgań sygnału sterowania serwonapędu [10].
Wyniki badań
Opisany algorytm sterowania ślizgowego został zaimplementowany w sterowniku rzeczywistego serwonapędu elektrohydraulicznego [10]. Badany układ składał się z siłownika hydraulicznego z dwustronnym tłoczyskiem oraz serwozaworu elektrohydraulicznego. Dla osiągnięcia efektywnej implementacji algorytmów sterowania wykorzystano komputer z zainstalowaną kartą kontrolno-pomiarową dSpace 1104 z procesorem sygnałowym DSP. Karta umożliwia konwersję sygnałów analogowych na cyfrowe (ADC), cyfrowych na analogowe (DAC), wyposażona jest w wejścia/wyjścia cyfrowe (I/O) oraz w n-koder i modulator o zmiennej szerokości impulsu (PWM). W odniesieniu do szerokości pasma przenoszenia serwozaworu oraz wymaganej dynamiki układu zamkniętego, czas próbkowania sterownika został ustalony na poziomie T = 1 ms.
Na rys. 2 przedstawiono odpowiedź skokową serwonapędu elektrohydraulicznego sterowanego ślizgowo z użyciem funkcji signum oraz sigmoidalnej. Porównanie przebiegu sygnału sterowania obu wariantów przedstawiono na rys. 3. Wybrano następujące wartości parametrów algorytmu ślizgowego: λ=6250, η=1500, φ=0,1.
Dla porównania jakości sterowania zaimplementowano również regulator PID o następujących parametrach: Kp=600, Ki=55, Kd=5. Na rys. 4 przedstawiono porównanie odchyłki nadążania w trakcie śledzenia sygnału sinusoidalnego przez algorytmy SMC i PID. Należy pamiętać, że jakość sterowania pozycyjnego w przypadku algorytmu ślizgowego zależy silnie od zjawiska przełączeń sygnału sterowania. Minimalizacja odchyłki jest osiągana kosztem większej liczby przełączeń.
Podsumowanie
Przedstawiono implementację algorytmu sterowania ślizgowego serwonapędu elektrohydraulicznego z wykorzystaniem funkcji signum i funkcji sigmoidalnej. Obie wersje algorytmu przebadano eksperymentalnie na stanowisku badawczym.
Wyniki badań udowodniły poprawę zachowań serwonapędu w przypadku sterowania ślizgowego wykorzystującego funkcję sigmoidalną (tanh), szczególnie przy niepewnych parametrach modelu oraz braku modelu tarcia.
W porównaniu z tradycyjnym regulatorem typu PID, wybrany wariant sterowania ślizgowego charakteryzuje się mniejszą odchyłką. Użycie funkcji sigmoidalnej w miejsce funkcji signum pozwala zminimalizować szkodliwe zjawisko szybkich przełączeń sygnału sterowania.
Bibliografia
- Helduser S., Mednis W., Olszewski M.: Elementy i układy hydrauliczne. Oficyna Wydawnicza PW, Warszawa 2009.
- Bonchis A., Corke P., Rye D., Ha Q.: Variable Structure Methods in Hydraulic Servo Systems Control. Automatica, 37 (2001), 589–595.
- Ha Q., Nguyen Q., Rye D., Durrant-Whyte H.: Fuzzy Sliding-Mode Controllers with Applications. IEEE Transactions On Industrial Electronics, 40 (2001) 1, 38–46.
- Ha, Q.: Sliding Performance Enhancing with Fuzzy Tuning. IEE Electronics Letters, 33 (1997) 16, 1421–1523.
- Liu Y., Handroos H.: Technical Note Sliding Mode Control for a Class of Hydraulic Position Servo. Mechatronics 9 (1999), 111–123.
- Perruquetti W., Barbot J.: Sliding Mode Control in Engineering. Marcel Dekker Inc., New York 2002.
- Slotine J.J., Sastry S.S.: Tracking Control of Nonlinear Systems Using Sliding Surfaces with Application to Robot Manipulators. Intern. Journal of Control, 39 (1983) 2, 465–492.
- Spurgeon S.K., Edwards C.: Sliding Mode Control. Taylor and Francis, London 1998.
- Winnicki A., Olszewski M.: Control of an Elektrohydraulic Position Servo System Using SMC. Hydraulica a Pneumatica, 24 (2006) 3–4, 27–29.
- Winnicki A., Olszewski M.: Sliding Mode Control of Electro-hydraulic Servo System. PAK, 55 (2009) 3, 174–177.
mgr inż. Arkadiusz Winnicki
Absolwent Wydziału Mechatroniki Politechniki Warszawskiej. Asystent w Zakładzie Urządzeń Wykonawczych Automatyki i Robotyki Instytutu Automatyki i Robotyki. W pracy naukowo-badawczej zajmuje się zagadnieniami algorytmów sterowania płynowymi urządzeniami wykonawczymi.
prof. nzw. dr hab. inż. Mariusz Olszewski
Absolwent, obecnie profesor, od 1994 r. dyrektor Instytutu Automatyki i Robotyki na Wydziale Mechatroniki Politechniki Warszawskiej, stypendysta niemieckiej Fundacji Alexandra v. Humboldta, członek konsorcjum Europejskiej Sieci Centrów Techniki Płynowej (FPCE). Staże naukowe w Reńsko-Westfalskiej Politechnice w Akwizgranie i Uniwersytecie Technicznym w Sztuttgarcie, praktyki w niemieckim przemyśle precyzyjnym imechatronicznym. Specjalista i autor publikacji, książek, podręczników, patentów i wdrożeń z zakresu budowy i sterowania urządzeń wykonawczych automatyki, robotyki przemysłowej i mechatroniki. Wieloletnia praktyka w kierowaniu krajowymi i międzynarodowymi projektami badawczymi i rozwojowymi.




![Rys. 1. Schemat budowy serwonapędu elektrohydraulicznego [Diagram of the structure of the electro-hydraulic servo system] Rys. 1. Schemat budowy serwonapędu elektrohydraulicznego [Diagram of the structure of the electro-hydraulic servo system]](/var/aol/storage/images/media/par/11_10/winnicki/1.jpg/77578-1-pol-PL/1.jpg_medium.jpg)
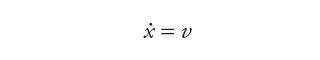
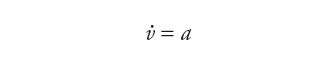
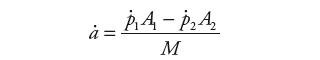
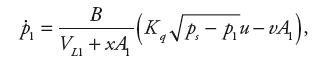
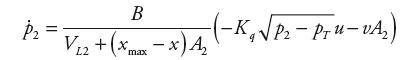
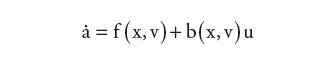
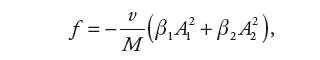
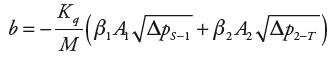
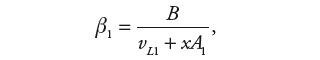
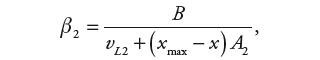
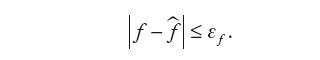
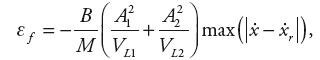
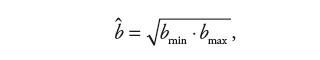
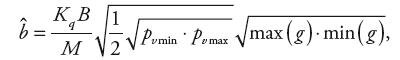
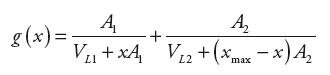
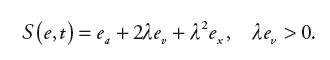
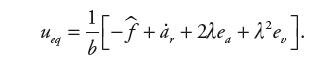
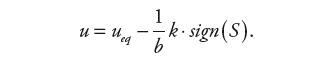
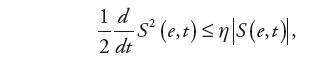
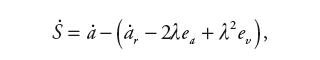
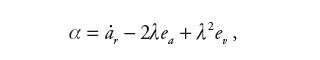
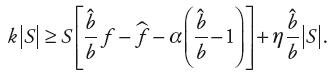
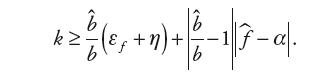
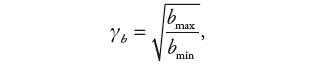
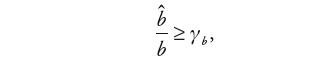
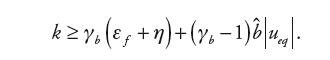
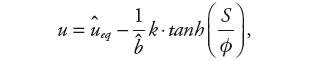
![Rys. 2. Odpowiedź skokowa serwonapędu elektrohydraulicznego sterowanego ślizgowo wykorzystaniem funkcji signum i sigmoidalne (tanh) [Step response of the slide mode controlled electro-hydraulic servo system with signum- and tanh-functions] Rys. 2. Odpowiedź skokowa serwonapędu elektrohydraulicznego sterowanego ślizgowo wykorzystaniem funkcji signum i sigmoidalne (tanh) [Step response of the slide mode controlled electro-hydraulic servo system with signum- and tanh-functions]](/var/aol/storage/images/media/par/11_10/winnicki/2.jpg/77662-1-pol-PL/2.jpg_medium.jpg)
![Rys. 3. Sygnał sterowania dla wymuszenia skokowego w dwóch wariantach sterowania ślizgowego z wykorzystaniem funkcji sigmoidalnej(tanh) i funkcji signum [Control signal for the step response in two variants of the slide mode control with signum- and tanh-functions] Rys. 3. Sygnał sterowania dla wymuszenia skokowego w dwóch wariantach sterowania ślizgowego z wykorzystaniem funkcji sigmoidalnej(tanh) i funkcji signum [Control signal for the step response in two variants of the slide mode control with signum- and tanh-functions]](/var/aol/storage/images/media/par/11_10/winnicki/3.jpg/77665-1-pol-PL/3.jpg_medium.jpg)
![Rys. 4. Odchyłka nadążania za sygnałem sinusoidalnym dla algorytmów sterowania SMC oraz PID [Position follow error with the sinusoidal signal for SMC- and PID-control] Rys. 4. Odchyłka nadążania za sygnałem sinusoidalnym dla algorytmów sterowania SMC oraz PID [Position follow error with the sinusoidal signal for SMC- and PID-control]](/var/aol/storage/images/media/par/11_10/winnicki/4.jpg/77668-1-pol-PL/4.jpg_medium.jpg)